Download Factoring Trinomials in the form x 2 + bx + c using Algebra Tiles

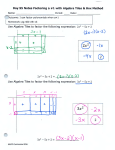
Factoring Trinomials in the form x2 + bx + c using Algebra Tiles
Student Activity
Materials:


Algebra Tiles
Worksheet: Factoring Trinomials using Algebra Tiles
Algebra Tiles:
Each algebra tile kit should contain three different sizes of tiles:
x by x tiles:
x2
1 by x tiles:
x
1 by 1 tiles:
1
The red tiles represent negative quantities and all other colors represent positive quantities.
The length of an “x” tile is unknown since “x” is a variable. Therefore, one cannot use “1 by 1” tiles
to match the length of an “x” tile.
Terminology:
Term: A number, a variable, or a product of numbers and/or variables. They are separated by addition signs.
Polynomial: An expression with more than one term.
Product:
Two or more numbers or terms that are multiplied.
Factors:
Terms that are multiplied
To Factor:
Rewrite a polynomial as a product
Prime:
An expression that cannot be factored
Lesson on factoring trinomials in the form x2 + bx + c:
Demonstration:
1.
In order to factor a trinomial such as x2 + 3x + 2, you first begin by gathering your tiles.
1 x2 tile, 3 x-tiles, and 2 unit tiles
2.
Arrange the tiles to form a perfect rectangle. This is like the inside of the multiplication table you
completed in a previous lab.
3.
The length and width of the above rectangle are like the outside of the multiplication table completed in a
previous lab. The length of this rectangle is (x + 2) and the width is (x + 1). The area of the rectangle is
length times width. Therefore, x2 + 3x + 2 = (x + 2)(x + 1)
Guided Practice:
Now try factoring x2 + 5x + 6.
1.
What tiles do you need to gather?
2.
Now form a rectangle using these tiles.
3.
What is the length of the rectangle?
4.
What is the width of the rectangle?
5.
How do the numbers 5 and 6 relate to the factored form?
****To check an answer, multiply the two binomial factors to see if they match the original trinomial.
Practice:
Use Algebra Tiles to factor the following trinomials. Remember, some trinomials do not factor. If it does not
factor, it is prime.
1.
x2 + 8x + 7
2.
x2 – 6x + 8
3.
x2 + 2x + 1
4.
x2 – 4x + 5
5.
x2 + 8x + 12
6.
x2 – 7x + 12
Reflection: Pattern Recognition
List at least 3 patterns you noticed when forming rectangles with the algebra tiles.
Pattern 1:
Pattern 2:
Pattern 3:
Suppose x2 + bx + c = (x + m)(x + n).
How are m and n related to b?
How are m and n related to c?