Algebraic Number Theory, a Computational Approach
... We will prove the theorem as follows. We first remark that any subgroup of a finitely generated free abelian group is finitely generated. Then we see that finitely generated abelian groups can be presented as quotients of finite rank free abelian groups, and such a presentation can be reinterpreted ...
... We will prove the theorem as follows. We first remark that any subgroup of a finitely generated free abelian group is finitely generated. Then we see that finitely generated abelian groups can be presented as quotients of finite rank free abelian groups, and such a presentation can be reinterpreted ...
CHAP03 Examples of Groups
... the groups are isomorphic. So ℤ12# is isomorphic to the mattress group but neither of these is isomorphic to ℤ10#. (We’ll define isomorphism a little more formally later.) So there are at least two, essentially different, groups of order 4. In fact, as we’ll see later, these are the only two. There ...
... the groups are isomorphic. So ℤ12# is isomorphic to the mattress group but neither of these is isomorphic to ℤ10#. (We’ll define isomorphism a little more formally later.) So there are at least two, essentially different, groups of order 4. In fact, as we’ll see later, these are the only two. There ...
STABLE COHOMOLOGY OF FINITE AND PROFINITE GROUPS 1
... contract to a subsimplex of ∆ which is a linear combination of different vertices of (g1 , . . . , gN ). Thus, we have natural contraction of EG to a ...
... contract to a subsimplex of ∆ which is a linear combination of different vertices of (g1 , . . . , gN ). Thus, we have natural contraction of EG to a ...
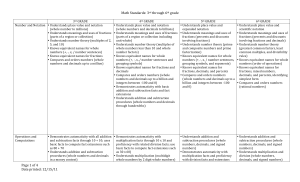
Math Standards: 3rd through 6th grade Page 1 of 4 Date printed: 12
... • Identifies and describes similar and congruent figures and describe their properties; constructs a figure that is congruent to another figure using a compass and straightedge • Identifies, describes, and sketches (including plotting on the coordinate plane) instances of reflections, trans ...
... • Identifies and describes similar and congruent figures and describe their properties; constructs a figure that is congruent to another figure using a compass and straightedge • Identifies, describes, and sketches (including plotting on the coordinate plane) instances of reflections, trans ...
EVERY CONNECTED SUM OF LENS SPACES IS A REAL
... such that M is diffeomorphic to a connected component of X(R). Corollary 1.2. Let M be a connected sum of finitely many lens spaces. Then, there is a uniruled real algebraic variety X such that M is diffeomorphic to a connected component of X(R). This proves Conjecture (2) above. Conjectures (3) and ...
... such that M is diffeomorphic to a connected component of X(R). Corollary 1.2. Let M be a connected sum of finitely many lens spaces. Then, there is a uniruled real algebraic variety X such that M is diffeomorphic to a connected component of X(R). This proves Conjecture (2) above. Conjectures (3) and ...