Chapter 5
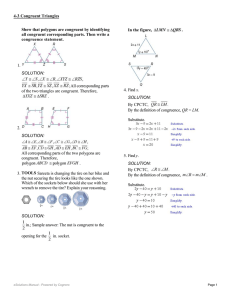
... about the origin and translate 3 units down. d. Sample answer: Reflect △ABC in the line y = x. 3. Look at the orientation of the original triangle and decide ...
... about the origin and translate 3 units down. d. Sample answer: Reflect △ABC in the line y = x. 3. Look at the orientation of the original triangle and decide ...
Chapter 3-Parallel and Perpendicular Lines
... 40. Write an equation in slope-intercept form of the line through point P(–10, 1) with slope –5. a. y = –5x – 49 b. y – 1 = –5(x + 10) c. y – 10 = –5(x + 1) d. y = –5x + 1 41. Write an equation in slope-intercept form of the line through points S(–10, –3) and T(–1, 1). ...
... 40. Write an equation in slope-intercept form of the line through point P(–10, 1) with slope –5. a. y = –5x – 49 b. y – 1 = –5(x + 10) c. y – 10 = –5(x + 1) d. y = –5x + 1 41. Write an equation in slope-intercept form of the line through points S(–10, –3) and T(–1, 1). ...
Geometry - School District of Clayton
... • Uses models to compare angles relative to right angles • Identifies right angles • Identifies corners (vertices) of cubes • Identifies the number of faces on rectangular prisms • Identifies and names a cylinder • Identifies and names a sphere • Sorts 2-D shapes and objects according to their attri ...
... • Uses models to compare angles relative to right angles • Identifies right angles • Identifies corners (vertices) of cubes • Identifies the number of faces on rectangular prisms • Identifies and names a cylinder • Identifies and names a sphere • Sorts 2-D shapes and objects according to their attri ...
The Geometry Lab PDF
... is an "undo" property that can be accessed by going to Edit at the top of the screen. You can use this to remove points you don't want. You can also remove points by right-clicking on them in the Algebra pane, and selecting "delete". Once you have 3 points, you should try to connect them to make a t ...
... is an "undo" property that can be accessed by going to Edit at the top of the screen. You can use this to remove points you don't want. You can also remove points by right-clicking on them in the Algebra pane, and selecting "delete". Once you have 3 points, you should try to connect them to make a t ...
1Topic
... a school in Alexandria during the reign of Ptolemy I, which lasted from 323 BC to 284 BC. Euclid’s most famous mathematical writing is the Elements. This work is the most complete study of geometry ever written and has been a major source of information for the study of geometric techniques, logic a ...
... a school in Alexandria during the reign of Ptolemy I, which lasted from 323 BC to 284 BC. Euclid’s most famous mathematical writing is the Elements. This work is the most complete study of geometry ever written and has been a major source of information for the study of geometric techniques, logic a ...
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3) for others. Euler angles are also used to describe the orientation of a frame of reference (typically, a coordinate system or basis) relative to another. They are typically denoted as α, β, γ, or φ, θ, ψ.Euler angles represent a sequence of three elemental rotations, i.e. rotations about the axes of a coordinate system. For instance, a first rotation about z by an angle α, a second rotation about x by an angle β, and a last rotation again about z, by an angle γ. These rotations start from a known standard orientation. In physics, this standard initial orientation is typically represented by a motionless (fixed, global, or world) coordinate system; in linear algebra, by a standard basis.Any orientation can be achieved by composing three elemental rotations. The elemental rotations can either occur about the axes of the fixed coordinate system (extrinsic rotations) or about the axes of a rotating coordinate system, which is initially aligned with the fixed one, and modifies its orientation after each elemental rotation (intrinsic rotations). The rotating coordinate system may be imagined to be rigidly attached to a rigid body. In this case, it is sometimes called a local coordinate system. Without considering the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups: Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y) Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z). Tait–Bryan angles are also called Cardan angles; nautical angles; heading, elevation, and bank; or yaw, pitch, and roll. Sometimes, both kinds of sequences are called ""Euler angles"". In that case, the sequences of the first group are called proper or classic Euler angles.