Distinguished Lecturer Series - Weizmann Institute of Science
... Maximal Dissipation in Equations of Evolution Abstract: The lecture will introduce examples of evolutionary equations with diverse provenances, in which a certain energy functional is conserved along classical solutions, the initial value problem generally admits a multitude of weak solutions, and a ...
... Maximal Dissipation in Equations of Evolution Abstract: The lecture will introduce examples of evolutionary equations with diverse provenances, in which a certain energy functional is conserved along classical solutions, the initial value problem generally admits a multitude of weak solutions, and a ...
Systems of Equations
... will show equations intersecting at only one point. d. Inconsistent System of Linear Equations – When a system of equations has no intersecting points then there is no solution and it is called Inconsistent. The graph of the system will show parallel lines. e. Dependent System of Linear Equations – ...
... will show equations intersecting at only one point. d. Inconsistent System of Linear Equations – When a system of equations has no intersecting points then there is no solution and it is called Inconsistent. The graph of the system will show parallel lines. e. Dependent System of Linear Equations – ...
MAXWELL`S EQUATIONS
... The electromagnetic theory was developed on the basis of electromagnetism with the help of four vector differential equations. These equations are known as Maxwell’s equations. Two of these relations are independent of time and are called as steady state equations. The other two relations depend u ...
... The electromagnetic theory was developed on the basis of electromagnetism with the help of four vector differential equations. These equations are known as Maxwell’s equations. Two of these relations are independent of time and are called as steady state equations. The other two relations depend u ...
We use Theorem 11.4, regarding the - Full
... ◗ Theorem 11.4 (Orthogonal families of level curves) Let φ (x, y) be harmonic in a domain D, let ψ (x, y) be the harmonic conjugate, and let F (z) = φ (x, y) + iψ (x, y) be the complex potential. Then the two families of level curves given in Equations (11-16) and (11-17), respectively, are orthogon ...
... ◗ Theorem 11.4 (Orthogonal families of level curves) Let φ (x, y) be harmonic in a domain D, let ψ (x, y) be the harmonic conjugate, and let F (z) = φ (x, y) + iψ (x, y) be the complex potential. Then the two families of level curves given in Equations (11-16) and (11-17), respectively, are orthogon ...
Revision
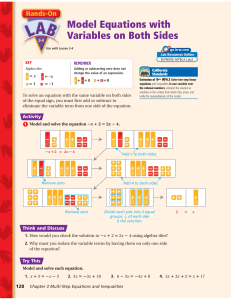
... what constitutes a solution. The students’ work above can be used to solve the quadratic (as will be seen in the Mathematical Foci which follow). However, x = x + 6 is not a solution in itself because it does not show what value of x ...
... what constitutes a solution. The students’ work above can be used to solve the quadratic (as will be seen in the Mathematical Foci which follow). However, x = x + 6 is not a solution in itself because it does not show what value of x ...
Introduction - Mars at UMHB
... ▫ Try collecting terms in the warm-up problem ▫ Expand sin(x-y) ▫ Factor the result of the collect command in the first example ...
... ▫ Try collecting terms in the warm-up problem ▫ Expand sin(x-y) ▫ Factor the result of the collect command in the first example ...