Document
... If we let y = the height of the branch, and z = the length of the rope, from the “before” picture, we may write: y z 2 since the branch must be two feet higher than the length of the rope. From the “after” picture, we may use the Pythagorean Theorem to write ( y 6) 2 82 z 2 . Substituting ...
... If we let y = the height of the branch, and z = the length of the rope, from the “before” picture, we may write: y z 2 since the branch must be two feet higher than the length of the rope. From the “after” picture, we may use the Pythagorean Theorem to write ( y 6) 2 82 z 2 . Substituting ...
Zanesville City Schools
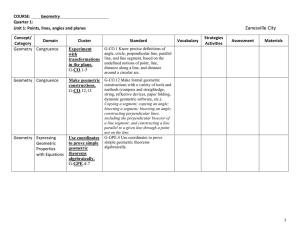
... parallel to a given line through a point not on the line. G-CO.13 Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. ...
... parallel to a given line through a point not on the line. G-CO.13 Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. ...
Geometry - USD 489
... Find arc lengths and areas of sectors of circles o Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. G.C.5 ...
... Find arc lengths and areas of sectors of circles o Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. G.C.5 ...
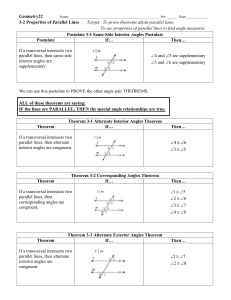
Lesson 3-2: Proving Lines Parallel
... 2 , 3 supplementary - a ║ b; converse same-side int angles theorem 4 , 8 supplementary - none; adjacent suppl angles not sufficient 1 3 - a ║ b; converse of corresponding angles post. 3 6 - a ║ b; converse of alt int angles theorem 1 6 - none; vertical angles not sufficient 11 7 ...
... 2 , 3 supplementary - a ║ b; converse same-side int angles theorem 4 , 8 supplementary - none; adjacent suppl angles not sufficient 1 3 - a ║ b; converse of corresponding angles post. 3 6 - a ║ b; converse of alt int angles theorem 1 6 - none; vertical angles not sufficient 11 7 ...
Geometry22 Name: Per: ______ Date: ______ 3
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.