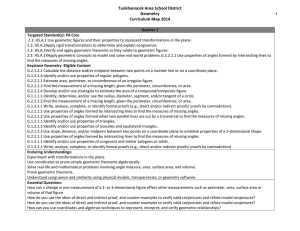
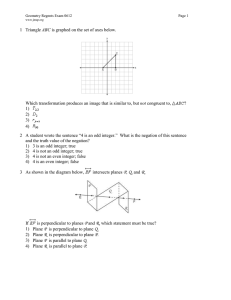
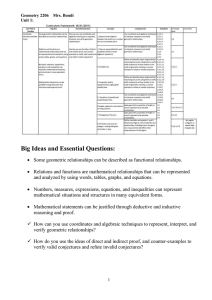
Chapter 4: Parallels - New Lexington City Schools
... photograph and to answer the questions below. Research For more information about photojournalism, visit: www.geomconcepts.com ...
... photograph and to answer the questions below. Research For more information about photojournalism, visit: www.geomconcepts.com ...
Name - North Penn School District
... Theorem 2-5 If two angles are both congruent and supplementary, then each is a right angle. ...
... Theorem 2-5 If two angles are both congruent and supplementary, then each is a right angle. ...
Investigating Geometry Activity: The Transitive Property of Parallel
... formed that is 498 and the one below it are supplementary. So, the angle below it is 1318. Since line n intersects line j, the angle formed that is 1318 and the one above it are supplementary. So, the angle above it is 498. Since a pair of corresponding angles are congruent, the lines m and n are pa ...
... formed that is 498 and the one below it are supplementary. So, the angle below it is 1318. Since line n intersects line j, the angle formed that is 1318 and the one above it are supplementary. So, the angle above it is 498. Since a pair of corresponding angles are congruent, the lines m and n are pa ...
Geometrical researches on the theory of parallels.
... of Schuyler's Geometry, which that author, like many of his unfortunate prototypes, then attempts to identify with Euclid's definition by pseudo-reasoning which tacitly assumes Euclid's postulate, e. g. he says p. 35: "For, if not parallel, they are not every where equally distant; and since they li ...
... of Schuyler's Geometry, which that author, like many of his unfortunate prototypes, then attempts to identify with Euclid's definition by pseudo-reasoning which tacitly assumes Euclid's postulate, e. g. he says p. 35: "For, if not parallel, they are not every where equally distant; and since they li ...
5.3 Parallel Lines and Congruent Angles
... 9 and 10 are a linear pair. So are 9 and 12 9 and 11 are vertical angles 9 and 7 are alternate exterior angles. So are 9 and 3 9 and 5 are corresponding angles. So are 9 and 1 ...
... 9 and 10 are a linear pair. So are 9 and 12 9 and 11 are vertical angles 9 and 7 are alternate exterior angles. So are 9 and 3 9 and 5 are corresponding angles. So are 9 and 1 ...
Riemannian connection on a surface

For the classical approach to the geometry of surfaces, see Differential geometry of surfaces.In mathematics, the Riemannian connection on a surface or Riemannian 2-manifold refers to several intrinsic geometric structures discovered by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early part of the twentieth century: parallel transport, covariant derivative and connection form . These concepts were put in their final form using the language of principal bundles only in the 1950s. The classical nineteenth century approach to the differential geometry of surfaces, due in large part to Carl Friedrich Gauss, has been reworked in this modern framework, which provides the natural setting for the classical theory of the moving frame as well as the Riemannian geometry of higher-dimensional Riemannian manifolds. This account is intended as an introduction to the theory of connections.