Angles as probabilities
... relative obscurity. But the answer is really much simpler than that, and here it is: The sum of the solid inner vertex angles of a tetrahedron T , divided by 2π, gives the probability that the orthogonal projection of T onto a random 2-plane is a triangle. How simple is that? We will prove a more ge ...
... relative obscurity. But the answer is really much simpler than that, and here it is: The sum of the solid inner vertex angles of a tetrahedron T , divided by 2π, gives the probability that the orthogonal projection of T onto a random 2-plane is a triangle. How simple is that? We will prove a more ge ...
Constructing graphs with given eigenvalues and angles
... graphs we got that usually only few pairs of vertices are not joined by fuzzy edge in the fuzzy image. Thus, the problem of the implementation of the edge condition still remains. ...
... graphs we got that usually only few pairs of vertices are not joined by fuzzy edge in the fuzzy image. Thus, the problem of the implementation of the edge condition still remains. ...
Notes on Rigidity Theory James Cruickshank
... to whether the corresponding edges of G are coloured black, white or not all. Now corresponding edges of P and Q are equal in length since the edge lengths of these polygons are essentially determined by the face angles of the faces in the polyhedra. Suppose that there are at most two colour changes ...
... to whether the corresponding edges of G are coloured black, white or not all. Now corresponding edges of P and Q are equal in length since the edge lengths of these polygons are essentially determined by the face angles of the faces in the polyhedra. Suppose that there are at most two colour changes ...
Regular polyhedra
... The goal of this worksheet is to understand regular polyhedra. According to wikipedia, a regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. Can you think of examples? A cube is a great example. One could naively expec ...
... The goal of this worksheet is to understand regular polyhedra. According to wikipedia, a regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. Can you think of examples? A cube is a great example. One could naively expec ...
A new class of graphs that satisfies the Chen
... least n distinct lines or has a universal line. The question is open for k ≥ 3. Aboulker et al. [2] proved that, for all k ≥ 3, a k-metric space with no universal line has at least n/5k distinct lines. A second type of metric space with integral distances arises from graphs. Any finite connected gra ...
... least n distinct lines or has a universal line. The question is open for k ≥ 3. Aboulker et al. [2] proved that, for all k ≥ 3, a k-metric space with no universal line has at least n/5k distinct lines. A second type of metric space with integral distances arises from graphs. Any finite connected gra ...
Day-34 Addendum: Polyhedral Surfaces Intro - Rose
... interpret the i, j entry equal 1 as there exists an edge between the points pi and pj . On the other hand if the entry is 0, there is no edge between pi and pj . With this set-up, the matrix will be symmetric aij = aji and the diagonal entries are zero aii = 0. The faces are represented as set of po ...
... interpret the i, j entry equal 1 as there exists an edge between the points pi and pj . On the other hand if the entry is 0, there is no edge between pi and pj . With this set-up, the matrix will be symmetric aij = aji and the diagonal entries are zero aii = 0. The faces are represented as set of po ...
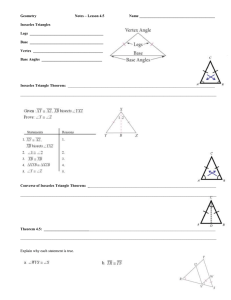
Name______________________________ Geometry Chapter 9
... 2) Suppose the points on the graph are translated using translation vector PQ. Find the components of vector PQ. ______________ Using translation vector PQ: Find the image of S’. __________ Find the image of (3, –2). ___________ Find the image of T’. __________ Find the image of U’. _________ 3) Gra ...
... 2) Suppose the points on the graph are translated using translation vector PQ. Find the components of vector PQ. ______________ Using translation vector PQ: Find the image of S’. __________ Find the image of (3, –2). ___________ Find the image of T’. __________ Find the image of U’. _________ 3) Gra ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑