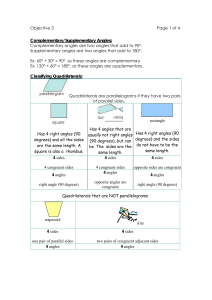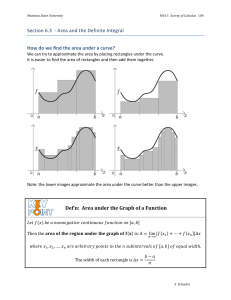
Section 6.3 -‐ Area and the Definite Integral How do we find the a
... Using Rectangles to Approximate Area under a Curve ...
... Using Rectangles to Approximate Area under a Curve ...
Course Outline
... use the finite difference process to determine the degree of a polynomial that generates a polynomial sequence determine the regression equation that generates a given sequence determine the explicit and recursive formulas that generate a given sequence ...
... use the finite difference process to determine the degree of a polynomial that generates a polynomial sequence determine the regression equation that generates a given sequence determine the explicit and recursive formulas that generate a given sequence ...
Mathematical Connections II Project 2
... 1. Make a triangle out of the strings/sticks of 3 different lengths that do not satisfy the Pythagorean Theorem (i.e. a 2 + b2 ≠ c 2 ) 2. Sketch a scaled drawing of this triangle. 3. Using a protractor, measure the angles between the sides. 4. Repeat steps (1) through (3) for at least two other tria ...
... 1. Make a triangle out of the strings/sticks of 3 different lengths that do not satisfy the Pythagorean Theorem (i.e. a 2 + b2 ≠ c 2 ) 2. Sketch a scaled drawing of this triangle. 3. Using a protractor, measure the angles between the sides. 4. Repeat steps (1) through (3) for at least two other tria ...
Course Outline for Precalculus_Mathematics
... Understand that if a determinant of a matrix is equal to zero, then the matrix does not have an inverse Use Cramer’s rule to solve a square system of linear equations Partial Fractions Decompose rational expressions into sums of partial fractions when the denominators contain: distinct linear ...
... Understand that if a determinant of a matrix is equal to zero, then the matrix does not have an inverse Use Cramer’s rule to solve a square system of linear equations Partial Fractions Decompose rational expressions into sums of partial fractions when the denominators contain: distinct linear ...
Platonic Geogami
... The Five Platonic Solids - What makes them so special? These are the only possible regular polyhedra. They are all regular solids. The same number of sides meet at the same angles at each vertex, and they have identical polygons that meet at the same angles at each edge. Each Platonic solid is also ...
... The Five Platonic Solids - What makes them so special? These are the only possible regular polyhedra. They are all regular solids. The same number of sides meet at the same angles at each vertex, and they have identical polygons that meet at the same angles at each edge. Each Platonic solid is also ...
Isosceles triangles are defined as having .
... ________: the two congruent sides ________: the third side __________ ___________: the angle opposite the base. __________ ___________: the angles adjacent to the base. Isosceles Triangle Theorem: If two sides of a triangle are congruent, then the __________ opposite those sides are congruen ...
... ________: the two congruent sides ________: the third side __________ ___________: the angle opposite the base. __________ ___________: the angles adjacent to the base. Isosceles Triangle Theorem: If two sides of a triangle are congruent, then the __________ opposite those sides are congruen ...
Honors Geometry Study Guide 1. Linear Pair 2. Vertical Angles 3
... a. soh - cah- toa b. To fInd a side: use sin, cos, or tan (angle given) = fraction c. To fInd a missing angle: use 2nd sin, cos, or tan (fraction) = A 14. Circles a. Equation of a circle: ( x-hi + (y-ki = f2 with center (h,k) and radius r b. Tangents 1. Perpendicular to the radius drawn to the point ...
... a. soh - cah- toa b. To fInd a side: use sin, cos, or tan (angle given) = fraction c. To fInd a missing angle: use 2nd sin, cos, or tan (fraction) = A 14. Circles a. Equation of a circle: ( x-hi + (y-ki = f2 with center (h,k) and radius r b. Tangents 1. Perpendicular to the radius drawn to the point ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑