Geometry22 Name: Per: ______ Date: ______ 3
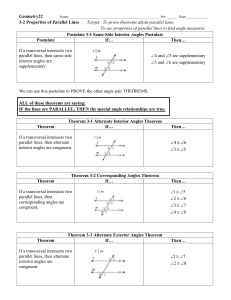
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
... ALL of these theorems are saying: IF the lines are PARALLEL, THEN the special angle relationships are true. ...
Geometry - Ch 7 - Quadrilaterals
... how many diagonals did you draw, and how many triangles were formed? ...
... how many diagonals did you draw, and how many triangles were formed? ...
Glossary∗
... Discrete graph A graph consisting of isolated or unconnected points, in contrast to a continuous graph. Divisor A factor of an integer. Example: 1, 2, 3, 4, 6, and 12 are the positive divisors of 12. Domain The set of values that can be used as inputs for a given function. Edge The line segment wher ...
... Discrete graph A graph consisting of isolated or unconnected points, in contrast to a continuous graph. Divisor A factor of an integer. Example: 1, 2, 3, 4, 6, and 12 are the positive divisors of 12. Domain The set of values that can be used as inputs for a given function. Edge The line segment wher ...
Definition: A triangle is the union of three segments (called its sides
... Definition: A triangle is the union of three segments (called its sides), whose endpoints (called its vertices) are taken, in pairs, from a set of three noncollinear points. Thus, if the vertices of a triangle are A, B and C, then its sides are ...
... Definition: A triangle is the union of three segments (called its sides), whose endpoints (called its vertices) are taken, in pairs, from a set of three noncollinear points. Thus, if the vertices of a triangle are A, B and C, then its sides are ...
CENTRAL TEXAS COLLEGE SYLLABUS FOR MATH
... Define radian measure and degree measure. ( F1, F2, F5, F6) Define the trigonometric functions using the unit circle. (F1, F2, F5, F6) Define the trigonometric functions using right angle trigonometry. (F1, F2, F5, F6) Graph the trigonometric functions. ( F2, F10) Define the inverse trigonometric fu ...
... Define radian measure and degree measure. ( F1, F2, F5, F6) Define the trigonometric functions using the unit circle. (F1, F2, F5, F6) Define the trigonometric functions using right angle trigonometry. (F1, F2, F5, F6) Graph the trigonometric functions. ( F2, F10) Define the inverse trigonometric fu ...
2d and 3d shapes
... Diagonals bisect at 90o Opposite angles are the same Adjacent angles sum to 180o Opposite sides are the same Opposite sides are parallel ...
... Diagonals bisect at 90o Opposite angles are the same Adjacent angles sum to 180o Opposite sides are the same Opposite sides are parallel ...
11-2 Chords and Arcs
... Note that the two parts of Theorem 11-5 are converses of each other. On p. 591, examine the proof of part 1 of Theorem 11-5 and note these special points from the following statement numbers. 4. Two triangles are proved congruent by HL. 5. What is another way to remember the isosceles triangle theor ...
... Note that the two parts of Theorem 11-5 are converses of each other. On p. 591, examine the proof of part 1 of Theorem 11-5 and note these special points from the following statement numbers. 4. Two triangles are proved congruent by HL. 5. What is another way to remember the isosceles triangle theor ...
What`s the Angle? - Discoveries About Convex
... The sum of the interior angles of an n-sided convex polygon can be found by the formula Sum = (n-2)*180, in which n is the number of sides of the polygon. This formula can be justified by the fact that any n-sided polygon can be divided into n-2 triangles by drawing diagonals from one of the vertice ...
... The sum of the interior angles of an n-sided convex polygon can be found by the formula Sum = (n-2)*180, in which n is the number of sides of the polygon. This formula can be justified by the fact that any n-sided polygon can be divided into n-2 triangles by drawing diagonals from one of the vertice ...
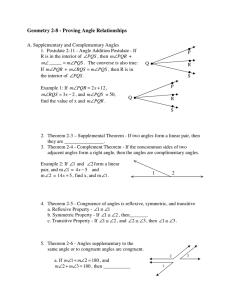
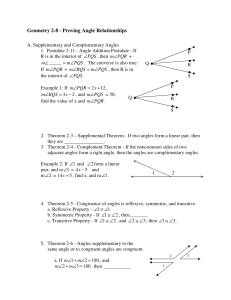
Geometry 2-8 - Proving Angle Relationships
... Geometry 2-8 - Proving Angle Relationships A. Supplementary and Complementary Angles 1. Postulate 2-11 - Angle Addition Postulate - If R is in the interior of ∠PQS , then m∠PQR + m∠ _____ = m∠PQS . The converse is also true: If m∠PQR + m∠RQS = m∠PQS , then R is in the interior of ∠PQS . Example 1: I ...
... Geometry 2-8 - Proving Angle Relationships A. Supplementary and Complementary Angles 1. Postulate 2-11 - Angle Addition Postulate - If R is in the interior of ∠PQS , then m∠PQR + m∠ _____ = m∠PQS . The converse is also true: If m∠PQR + m∠RQS = m∠PQS , then R is in the interior of ∠PQS . Example 1: I ...
Math 2 Geometry Based on Elementary Geometry, 3rd ed, by
... Use the formula to find the number of diagonals of: ...
... Use the formula to find the number of diagonals of: ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑