3.1 What are congruent figures?
... Where is the longest side located? The shortest? If base angles are congruent what can we say about the triangle? ...
... Where is the longest side located? The shortest? If base angles are congruent what can we say about the triangle? ...
pdf Version
... however, incomplete. It would be complete if he also included the condition that each vertex should join equal number of faces. There exist five more polyhedra satisfying Euclid’s original definition: five of the deltahedra. Deltahedra are equilateral triangle faced convex polyhedra. There are total ...
... however, incomplete. It would be complete if he also included the condition that each vertex should join equal number of faces. There exist five more polyhedra satisfying Euclid’s original definition: five of the deltahedra. Deltahedra are equilateral triangle faced convex polyhedra. There are total ...
Solutions to suggested problems.
... also a theorem of the system.” So, we have infact five theorems to work with (and nothing else). Theorem Theorem Theorem Theorem Theorem ...
... also a theorem of the system.” So, we have infact five theorems to work with (and nothing else). Theorem Theorem Theorem Theorem Theorem ...
Chapter 5 Review
... possible lengths of side OM, so that there are zero, one or two triangles that satisfy these conditions. Draw each triangle to support your answer. ...
... possible lengths of side OM, so that there are zero, one or two triangles that satisfy these conditions. Draw each triangle to support your answer. ...
More on Neutral Geometry I (Including Section 3.3) ( "NIB" means
... Suppose, by way of contradiction, that AC and DF are not congruent . ∴ AC ≠ DF . Without loss of generality, we assume that AC > DF . [ Note: If AC < DF , then we rename the points A, B, C as D, E, F, and we rename the points D, E, F as A, B, C , respectively. After these renamings, every statement ...
... Suppose, by way of contradiction, that AC and DF are not congruent . ∴ AC ≠ DF . Without loss of generality, we assume that AC > DF . [ Note: If AC < DF , then we rename the points A, B, C as D, E, F, and we rename the points D, E, F as A, B, C , respectively. After these renamings, every statement ...
Honors Geometry Unit 2B Review Quads To be successful on this
... Below are some problems for you to practice before the exam. Not every type of problem on the exam is represented here, however these problems will allow you to refresh your memory on some concepts that you will see on the exam. It is in your best interest to use your class notes and examples as wel ...
... Below are some problems for you to practice before the exam. Not every type of problem on the exam is represented here, however these problems will allow you to refresh your memory on some concepts that you will see on the exam. It is in your best interest to use your class notes and examples as wel ...
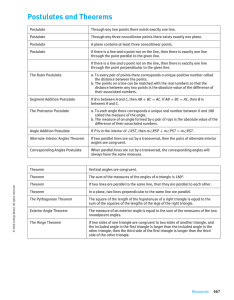
Postulates and Theorems, Geometry Honors
... a. To every pair of points there corresponds a unique positive number called the distance between the points. b. The points on a line can be matched with the real numbers so that the distance between any two points is the absolute value of the difference of their associated numbers. ...
... a. To every pair of points there corresponds a unique positive number called the distance between the points. b. The points on a line can be matched with the real numbers so that the distance between any two points is the absolute value of the difference of their associated numbers. ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑