Olymon Volume 1 - Department of Mathematics, University of Toronto
... of the University of Alberta and Valeria Pandeleva in Ottawa. Notes: The inradius of a triangle is the radius of the incircle, the circle that touches each side of the polygon. The circumradius of a triangle is the radius of the circumcircle, the circle that passes through its three vertices. A set ...
... of the University of Alberta and Valeria Pandeleva in Ottawa. Notes: The inradius of a triangle is the radius of the incircle, the circle that touches each side of the polygon. The circumradius of a triangle is the radius of the circumcircle, the circle that passes through its three vertices. A set ...
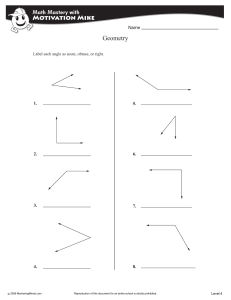
Geometry - 4thGrade
... 1. Line K is parallel to line M. 2. Line J is parallel to line K. 3. Line L is perpendicular to line J. 4. Line M is perpendicular to line N. 5. Line L is parallel to line N. 6. Line P is parallel to line L. 7. Line L is parallel to line J. 8. Line P is perpendicular to line K. 9. Line M is parallel ...
... 1. Line K is parallel to line M. 2. Line J is parallel to line K. 3. Line L is perpendicular to line J. 4. Line M is perpendicular to line N. 5. Line L is parallel to line N. 6. Line P is parallel to line L. 7. Line L is parallel to line J. 8. Line P is perpendicular to line K. 9. Line M is parallel ...
Right Triangle
... triangles apart. They look exactly the same. One triangle could be picked up and put on top of the other. A ...
... triangles apart. They look exactly the same. One triangle could be picked up and put on top of the other. A ...
After this lesson, you should be able to:
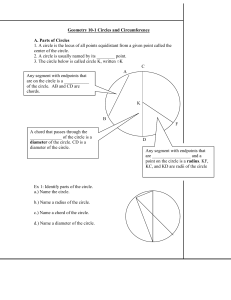
... 3. Tangent segment – the part of the tangent line between the point of contact and a point outside the circle. a. Name the tangent segment in the diagram. 4. Secant segment – the part of a secant line that joins a point outside the circle to the farther intersection point of the secant and the circl ...
... 3. Tangent segment – the part of the tangent line between the point of contact and a point outside the circle. a. Name the tangent segment in the diagram. 4. Secant segment – the part of a secant line that joins a point outside the circle to the farther intersection point of the secant and the circl ...
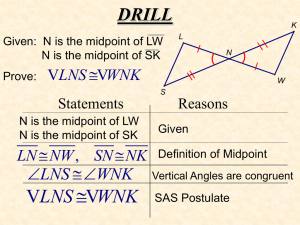
Section 2-8 - winegardnermathclass
... Review: Supplementary angles add up to 180. Complementary angles add up to 90. Congruent angles have the same measure. Vertical angles are congruent. New Postulates and Theorems: Postulate 2.10 (Protractor Postulate) Given ray AB and a number r between 0 and 180, there is exactly one ray with endpoi ...
... Review: Supplementary angles add up to 180. Complementary angles add up to 90. Congruent angles have the same measure. Vertical angles are congruent. New Postulates and Theorems: Postulate 2.10 (Protractor Postulate) Given ray AB and a number r between 0 and 180, there is exactly one ray with endpoi ...
IMO 2006 Shortlisted Problems - International Mathematical Olympiad
... be nonzero. There exist representations of ψx + y of the form ψx + y = ψ i1 + · · · + ψ ik where i1 ≤ · · · ≤ ik is a sequence of nonnegative integers, not necessarily distinct. For instance, we can take x summands ψ 1 = ψ and y summands ψ 0 = 1. Consider all such representations of minimum length k ...
... be nonzero. There exist representations of ψx + y of the form ψx + y = ψ i1 + · · · + ψ ik where i1 ≤ · · · ≤ ik is a sequence of nonnegative integers, not necessarily distinct. For instance, we can take x summands ψ 1 = ψ and y summands ψ 0 = 1. Consider all such representations of minimum length k ...
Math Glossary - Bedminster School
... divisible by its factors. For example, 4 and 7 are factors of 28 because 4 * 7 = 28, and 28 is divisible by 4 and 7. factor pair Two whole-number factors of a number n whose product is the number n. A number may have more than one factor pair. For example, the factor pairs for 21 are 1 and 21, and 3 ...
... divisible by its factors. For example, 4 and 7 are factors of 28 because 4 * 7 = 28, and 28 is divisible by 4 and 7. factor pair Two whole-number factors of a number n whose product is the number n. A number may have more than one factor pair. For example, the factor pairs for 21 are 1 and 21, and 3 ...
Neutral Geometry Theorems Theorem 1. Every line segment has a
... Corollary 40. Given three distinct non-collinear points in a plane, there is a unique circle containing these points. Theorem 41. A point is on an angle bisector if and only if it is interior to the angle and equidistant from the sides of the angle. ...
... Corollary 40. Given three distinct non-collinear points in a plane, there is a unique circle containing these points. Theorem 41. A point is on an angle bisector if and only if it is interior to the angle and equidistant from the sides of the angle. ...
Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the (simple) 3-vertex-connected planar graphs (with at least four vertices). That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs. Steinitz's theorem is named after Ernst Steinitz, who submitted its first proof for publication in 1916. Branko Grünbaum has called this theorem “the most important and deepest known result on 3-polytopes.”The name ""Steinitz's theorem"" has also been applied to other results of Steinitz: the Steinitz exchange lemma implying that each basis of a vector space has the same number of vectors, the theorem that if the convex hull of a point set contains a unit sphere, then the convex hull of a finite subset of the point contains a smaller concentric sphere, and Steinitz's vectorial generalization of the Riemann series theorem on the rearrangements of conditionally convergent series.↑ ↑ 2.0 2.1 ↑ ↑ ↑ ↑ ↑ ↑ ↑ ↑