Quadrilaterals Theorems Ptolemy`s Theorem
... 1. If a line cuts a tangential quadrilateral into two polygons with equal areas and equal perimeters, the line passes through the incenter 2. If M and N are midpoints of diagonals and incenter = I, then M, I, and N are ...
... 1. If a line cuts a tangential quadrilateral into two polygons with equal areas and equal perimeters, the line passes through the incenter 2. If M and N are midpoints of diagonals and incenter = I, then M, I, and N are ...
Unit 1 – Transformations Terms and Definitions
... A line is a straight, continuous arrangement of infinitely many points. It is infinitely long and extends in two directions but has no width or thickness. It is represented and named by any two distinct points that lie on it. A plane has length and width but no thickness. It is a flat surface that e ...
... A line is a straight, continuous arrangement of infinitely many points. It is infinitely long and extends in two directions but has no width or thickness. It is represented and named by any two distinct points that lie on it. A plane has length and width but no thickness. It is a flat surface that e ...
File
... A square is a quadrilateral with four right angles and four congruent sides. In the exercises, you will show that a square is a parallelogram, a rectangle, and a rhombus. So a square has the properties of all three. ...
... A square is a quadrilateral with four right angles and four congruent sides. In the exercises, you will show that a square is a parallelogram, a rectangle, and a rhombus. So a square has the properties of all three. ...
Trainer/Instructor Notes: Transformations Terms and
... and extends in two directions but has no width or thickness. It is represented and named by any two distinct points that lie on it. A plane has length and width but no thickness. It is a flat surface that extends infinitely along its length and width. It can be named with a script capital letter, su ...
... and extends in two directions but has no width or thickness. It is represented and named by any two distinct points that lie on it. A plane has length and width but no thickness. It is a flat surface that extends infinitely along its length and width. It can be named with a script capital letter, su ...
Circle geometry
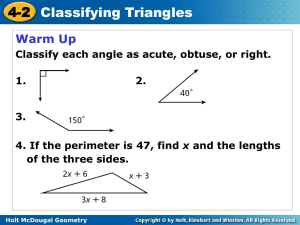
... Find the values of the pronumerals in each of the following figures, giving reasons for your answers. ...
... Find the values of the pronumerals in each of the following figures, giving reasons for your answers. ...
Student Name________________________________ Instructor
... 7. Be able to find the vertices and asymptotes of a hyperbola. 8. Be able to find important values (foci, directrix, vertices, asymptotes) for conic functions subjected to horizontal and vertical shifts. 9. Be able to graph and find the general equation of a shifted conic section. 10. Be able to the ...
... 7. Be able to find the vertices and asymptotes of a hyperbola. 8. Be able to find important values (foci, directrix, vertices, asymptotes) for conic functions subjected to horizontal and vertical shifts. 9. Be able to graph and find the general equation of a shifted conic section. 10. Be able to the ...
Math: Geometry: Geometric Measurement and Dimension
... Calculates the volume of a rectangular prism, and converts to a different measurement scale (customary units) Classifies polygons by type of angle Describes the change in area of a triangle when 1 dimension of an object is altered (metric units) Describes the change in perimeter when dimensions of a ...
... Calculates the volume of a rectangular prism, and converts to a different measurement scale (customary units) Classifies polygons by type of angle Describes the change in area of a triangle when 1 dimension of an object is altered (metric units) Describes the change in perimeter when dimensions of a ...
Analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.Analytic geometry is widely used in physics and engineering, and is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and squares, often in two and sometimes in three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space (three dimensions). As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometrical shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. The numerical output, however, might also be a vector or a shape. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.