PROFESSOR SMITH MATH 295 LECTURE NOTES 1. November 2
... Theorem 1.1. A subset S of the real line is compact (in the Euclidean topology) if and only if S is closed and bounded. Proof. We proved yesterday that compact implies closed and bounded. It remains only to prove the other direction, that a closed bounded set is always compact. The hardest part is t ...
... Theorem 1.1. A subset S of the real line is compact (in the Euclidean topology) if and only if S is closed and bounded. Proof. We proved yesterday that compact implies closed and bounded. It remains only to prove the other direction, that a closed bounded set is always compact. The hardest part is t ...
S2 - WVU Math Department
... 3. Any finite collection of points, E = {x(1) , . . . , x(m) } is closed in in Rn . 4. Let E = (x(k) ), be the points of a convergent sequence in Rn . Then E is neither open nor closed. E has no interior, i.e., E 0 = ∅. E − = E ∪ {x∗ } where x(k) → x∗ as k → ∞. The last example again motivates a def ...
... 3. Any finite collection of points, E = {x(1) , . . . , x(m) } is closed in in Rn . 4. Let E = (x(k) ), be the points of a convergent sequence in Rn . Then E is neither open nor closed. E has no interior, i.e., E 0 = ∅. E − = E ∪ {x∗ } where x(k) → x∗ as k → ∞. The last example again motivates a def ...
Homework 5 (pdf)
... Do any 5 of the 8 problems. Each problem is worth 20 points. Solutions will be graded for correctness, clarity and style. (1) Let X be a topological space. If C is a finite subset of X, show that C is compact. (2) Let X be a set with the discrete topology. If C ⊆ X is compact, show that C is finite. ...
... Do any 5 of the 8 problems. Each problem is worth 20 points. Solutions will be graded for correctness, clarity and style. (1) Let X be a topological space. If C is a finite subset of X, show that C is compact. (2) Let X be a set with the discrete topology. If C ⊆ X is compact, show that C is finite. ...
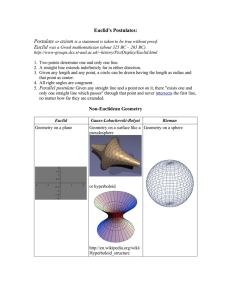
Euclid`s Postulates
... 1. Two points determine one and only one line. 2. A straight line extends indefinitely far in either direction. 3. Given any length and any point, a circle can be drawn having the length as radius and that point as center. 4. All right angles are congruent. 5. Parallel postulate Given any straight l ...
... 1. Two points determine one and only one line. 2. A straight line extends indefinitely far in either direction. 3. Given any length and any point, a circle can be drawn having the length as radius and that point as center. 4. All right angles are congruent. 5. Parallel postulate Given any straight l ...
Problem 1: We denote the usual “Euclidean” metric on IRn by de : |x
... Problems 6-9 are not hard and not long (I resisted saying “are short and easy” :)); we’re just trying to give some exercises not entirely in the book. You are also learning a tad more about the product topology and such, which we won’t do formally in lecture. Problem 6: Let X, Y be topological space ...
... Problems 6-9 are not hard and not long (I resisted saying “are short and easy” :)); we’re just trying to give some exercises not entirely in the book. You are also learning a tad more about the product topology and such, which we won’t do formally in lecture. Problem 6: Let X, Y be topological space ...
Lectures on Klein surfaces and their fundamental group.
... associated an orientable (in fact, oriented) real surface, i.e. a two-dimensional manifold. Conversely, any compact, connected, orientable surface admits a structure of complex analytic manifold of dimension one (i.e. a Riemann surface structure), with respect to which it embeds onto a complex subma ...
... associated an orientable (in fact, oriented) real surface, i.e. a two-dimensional manifold. Conversely, any compact, connected, orientable surface admits a structure of complex analytic manifold of dimension one (i.e. a Riemann surface structure), with respect to which it embeds onto a complex subma ...
Curves and Manifolds
... theory of plane curves of degree 3 is already very deep, and connected with the Weierstrass's theory of bi-periodic complex analytic functions (cf. elliptic curves, Weierstrass P-function). There are many questions in the theory of plane algebraic curves for which the answer is not known as of the b ...
... theory of plane curves of degree 3 is already very deep, and connected with the Weierstrass's theory of bi-periodic complex analytic functions (cf. elliptic curves, Weierstrass P-function). There are many questions in the theory of plane algebraic curves for which the answer is not known as of the b ...
Tutorial Sheet 6, Topology 2011
... Solution: It is not discrete because {p/q} is not open – if it was {p/q} = U ∩ Q for some open set U ⊂ R. But this isn’t possible - the rational numbers are dense, so any open ball contains infinitely many of them. To see that it is totally disconnected, let C be a component containing two points, x ...
... Solution: It is not discrete because {p/q} is not open – if it was {p/q} = U ∩ Q for some open set U ⊂ R. But this isn’t possible - the rational numbers are dense, so any open ball contains infinitely many of them. To see that it is totally disconnected, let C be a component containing two points, x ...
TOPOLOGICAL PROOFS OF THE EXTREME AND INTERMEDIATE
... Definition 1.3. A set B is called closed if its complement is open. A closed interval from a to b in R with a < b is denoted [a, b]. Definition 1.4. Let S be a subset of a topological space X. A point p in X is called a limit point of S if every open set containing p also contains a point of S other ...
... Definition 1.3. A set B is called closed if its complement is open. A closed interval from a to b in R with a < b is denoted [a, b]. Definition 1.4. Let S be a subset of a topological space X. A point p in X is called a limit point of S if every open set containing p also contains a point of S other ...
TOPOLOGY 1. Introduction By now, we`ve seen many uses of
... map f : X → Y is said to be continuous if for all open sets V ∈ Y , f −1 (V ) is an open set in X. If in addition f is bijective (that is, one to one and onto) and f −1 is continuous, f is called a homeomorphism and (X, T ) and (Y, S) are said to be homeomorphic as topological spaces. One way to thi ...
... map f : X → Y is said to be continuous if for all open sets V ∈ Y , f −1 (V ) is an open set in X. If in addition f is bijective (that is, one to one and onto) and f −1 is continuous, f is called a homeomorphism and (X, T ) and (Y, S) are said to be homeomorphic as topological spaces. One way to thi ...
Presentation can be downloaded here.
... • An ideal black body has emissivity 1 and it is independent of temperature. For a glass bulb,the power received at the surface is a fraction of the power emitted by filament.This fraction remains constant with temperature. Temperature resistance constant, R/Ro=Resistance to Room temperature, TO=Roo ...
... • An ideal black body has emissivity 1 and it is independent of temperature. For a glass bulb,the power received at the surface is a fraction of the power emitted by filament.This fraction remains constant with temperature. Temperature resistance constant, R/Ro=Resistance to Room temperature, TO=Roo ...
PDF
... confusion, α(g, x) is simply written gx, so that the two conditions above read 1x = x and (g1 g2 )x = g1 (g2 x). If a topological transformation group G on X is effective, then G can be viewed as a group of homeomorphisms on X: simply define hg : X → X by hg (x) = gx for each g ∈ G so that hg is the ...
... confusion, α(g, x) is simply written gx, so that the two conditions above read 1x = x and (g1 g2 )x = g1 (g2 x). If a topological transformation group G on X is effective, then G can be viewed as a group of homeomorphisms on X: simply define hg : X → X by hg (x) = gx for each g ∈ G so that hg is the ...
Topological models in holomorphic dynamics - IME-USP
... Summary: application to the case of quadratic dynamics Pc : z 7→ z2 + c Main object to study: ”Filled Julia set Kc ” (for a given c) Kc+ := {z ∈ C|orbit of z is bounded} Strong dichotomy: (recall that M := {c ∈ C|orbit of c is bounded}) Case c ∈ M: then Kc is connected (but not necessarily loc. con ...
... Summary: application to the case of quadratic dynamics Pc : z 7→ z2 + c Main object to study: ”Filled Julia set Kc ” (for a given c) Kc+ := {z ∈ C|orbit of z is bounded} Strong dichotomy: (recall that M := {c ∈ C|orbit of c is bounded}) Case c ∈ M: then Kc is connected (but not necessarily loc. con ...