END
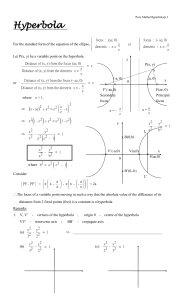
... Four points P1 , P2 , P3 and P4 on the hyperbola have parameters t1 , t2 , t3 and t4 respectively. (a) Prove that P1 , P2 , P3 and P4 lie on a circle if and only if t1 t2 t3 t4 = 1 . (b) State the relationship between the hyperbola and the circle through the points P1, P3 and P4 if t12 t3 t4 = 1 . ( ...
... Four points P1 , P2 , P3 and P4 on the hyperbola have parameters t1 , t2 , t3 and t4 respectively. (a) Prove that P1 , P2 , P3 and P4 lie on a circle if and only if t1 t2 t3 t4 = 1 . (b) State the relationship between the hyperbola and the circle through the points P1, P3 and P4 if t12 t3 t4 = 1 . ( ...
The Inverse of a Matrix
... exactly one solution, infinitely many solutions, or no solution. If the coefficient matrix A of a square system (a system that has the same number of equations as variables) is invertible, the system has a unique solution, which is defined as follows. ...
... exactly one solution, infinitely many solutions, or no solution. If the coefficient matrix A of a square system (a system that has the same number of equations as variables) is invertible, the system has a unique solution, which is defined as follows. ...
IOSR Journal of Applied Physics (IOSR-JAP)
... n=0,1,2,3... For Venus, Earth …etc. The value we get when n=3 is assign to Asteroids. Here I am trying to generate an equation to find the straight line distance of first eight planets from sun, via combining Classical Physics with Number Theory. The weapon we are taking from number theory is Mainly ...
... n=0,1,2,3... For Venus, Earth …etc. The value we get when n=3 is assign to Asteroids. Here I am trying to generate an equation to find the straight line distance of first eight planets from sun, via combining Classical Physics with Number Theory. The weapon we are taking from number theory is Mainly ...
Equation

In mathematics, an equation is an equality containing one or more variables. Solving the equation consists of determining which values of the variables make the equality true. In this situation, variables are also known as unknowns and the values which satisfy the equality are known as solutions. An equation differs from an identity in that an equation is not necessarily true for all possible values of the variable.There are many types of equations, and they are found in all areas of mathematics; the techniques used to examine them differ according to their type.Algebra studies two main families of equations: polynomial equations and, among them, linear equations. Polynomial equations have the form P(X) = 0, where P is a polynomial. Linear equations have the form a(x) + b = 0, where a is a linear function and b is a vector. To solve them, one uses algorithmic or geometric techniques, coming from linear algebra or mathematical analysis. Changing the domain of a function can change the problem considerably. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.Geometry uses equations to describe geometric figures. The objective is now different, as equations are used to describe geometric properties. In this context, there are two large families of equations, Cartesian equations and parametric equations.Differential equations are equations involving one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model real-life processes in areas such as physics, chemistry, biology, and economics.The ""="" symbol was invented by Robert Recorde (1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.