Systems of Equations
... 1. First the two equations need to be in standard form and the like terms added up. 2. Then multiply one or both equations until you get two opposite like terms. 3. Add the two equations. 4. Solve for the first variable. 5. Plug the first variable back in to find the other variable. 6.Plug your answ ...
... 1. First the two equations need to be in standard form and the like terms added up. 2. Then multiply one or both equations until you get two opposite like terms. 3. Add the two equations. 4. Solve for the first variable. 5. Plug the first variable back in to find the other variable. 6.Plug your answ ...
Fall 2013 Slides for Math Camp – Day 1
... • Input: independent variable, exogenous variable, x or t • Output: dependent variable, endogenous variable, y So, y equals some function of x (or t) y = f(x) f is often used as the notation for a function but it is not a must g(x), v(t) ...
... • Input: independent variable, exogenous variable, x or t • Output: dependent variable, endogenous variable, y So, y equals some function of x (or t) y = f(x) f is often used as the notation for a function but it is not a must g(x), v(t) ...
ALGEBRA-----CHAPTER 5 RELAY GAME
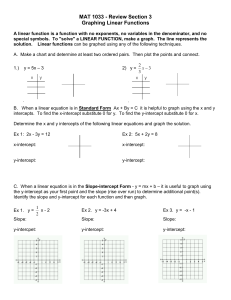
... 14. Find the equation of the line passing thru ( 1 , 2 ) and ( 6 , - 8 ) in standard form. 15. Find the equation of the line with x-intercept of 2 and y-intercept of – 6 in standard form. 16. Find the equation of the line parallel to the graph of y = 1/5 x – 10 passing thru the point ( - 4 , 6 ). W ...
... 14. Find the equation of the line passing thru ( 1 , 2 ) and ( 6 , - 8 ) in standard form. 15. Find the equation of the line with x-intercept of 2 and y-intercept of – 6 in standard form. 16. Find the equation of the line parallel to the graph of y = 1/5 x – 10 passing thru the point ( - 4 , 6 ). W ...
Solving Systems of Linear Equations by Elimination
... Using the addition property to solve systems is called the elimination method. With this method, the idea is to eliminate one of the variables. To do this, one pair of variable terms in the two equations must have coefficients that are opposite. Slide 4.3-4 ...
... Using the addition property to solve systems is called the elimination method. With this method, the idea is to eliminate one of the variables. To do this, one pair of variable terms in the two equations must have coefficients that are opposite. Slide 4.3-4 ...
B-4 Writing Linear Equations
... y = – 3x + 4, or, in standard form, 3x + y = 4. In previous courses you have also learned that the slope-intercept form can be used to find an equation of a line given the slope and the coordinates of any point on the line. ...
... y = – 3x + 4, or, in standard form, 3x + y = 4. In previous courses you have also learned that the slope-intercept form can be used to find an equation of a line given the slope and the coordinates of any point on the line. ...
Critical Thinking Math HS Exit-Level Sample Questions
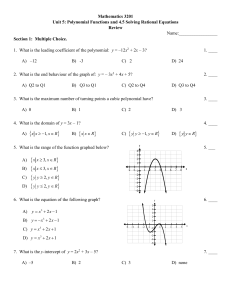
... Rochelle bought a picnic table on sale for 50% off the original price. The store charged her 10% tax, and her final cost was $22.00. Rochelle would like to know the original price of the picnic table. What is an equation that can be used to solve the problem if x = the original price? A) 0.10(x + 0. ...
... Rochelle bought a picnic table on sale for 50% off the original price. The store charged her 10% tax, and her final cost was $22.00. Rochelle would like to know the original price of the picnic table. What is an equation that can be used to solve the problem if x = the original price? A) 0.10(x + 0. ...
Equation

In mathematics, an equation is an equality containing one or more variables. Solving the equation consists of determining which values of the variables make the equality true. In this situation, variables are also known as unknowns and the values which satisfy the equality are known as solutions. An equation differs from an identity in that an equation is not necessarily true for all possible values of the variable.There are many types of equations, and they are found in all areas of mathematics; the techniques used to examine them differ according to their type.Algebra studies two main families of equations: polynomial equations and, among them, linear equations. Polynomial equations have the form P(X) = 0, where P is a polynomial. Linear equations have the form a(x) + b = 0, where a is a linear function and b is a vector. To solve them, one uses algorithmic or geometric techniques, coming from linear algebra or mathematical analysis. Changing the domain of a function can change the problem considerably. Algebra also studies Diophantine equations where the coefficients and solutions are integers. The techniques used are different and come from number theory. These equations are difficult in general; one often searches just to find the existence or absence of a solution, and, if they exist, to count the number of solutions.Geometry uses equations to describe geometric figures. The objective is now different, as equations are used to describe geometric properties. In this context, there are two large families of equations, Cartesian equations and parametric equations.Differential equations are equations involving one or more functions and their derivatives. They are solved by finding an expression for the function that does not involve derivatives. Differential equations are used to model real-life processes in areas such as physics, chemistry, biology, and economics.The ""="" symbol was invented by Robert Recorde (1510–1558), who considered that nothing could be more equal than parallel straight lines with the same length.