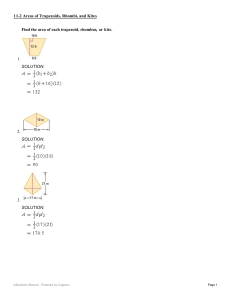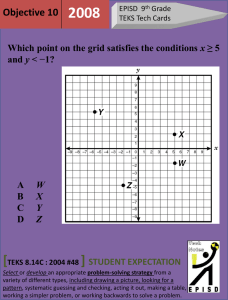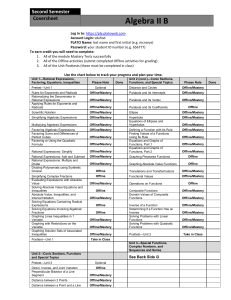
Garrett 09-23-2011 1 Continuing the pre/review of the simple (!?) case... Some
... want. From xn we can recover all the earlier ones: xn−1 , xn−2 , . . . , x2 , x1 , at least modulo the respective pk ’s. It would be conceptually economical if the sequence x1 , x2 , x3 , . . . had a limit, x∞ , which somehow solved the equation modulo p∞ , from which we could recover solutions modu ...
... want. From xn we can recover all the earlier ones: xn−1 , xn−2 , . . . , x2 , x1 , at least modulo the respective pk ’s. It would be conceptually economical if the sequence x1 , x2 , x3 , . . . had a limit, x∞ , which somehow solved the equation modulo p∞ , from which we could recover solutions modu ...
Full text
... the squares of its decimal digits. For a E Z + , let 82(a) — a and for m > 1 let S'2h(a) = S2(S™~1(a)). A happy number is a positive integer a such that 5™ (a) — 1 for some m > 0. It is well known that 4 is not a happy number and that, in fact, for all a £ Z + , a is not a happy number if and only i ...
... the squares of its decimal digits. For a E Z + , let 82(a) — a and for m > 1 let S'2h(a) = S2(S™~1(a)). A happy number is a positive integer a such that 5™ (a) — 1 for some m > 0. It is well known that 4 is not a happy number and that, in fact, for all a £ Z + , a is not a happy number if and only i ...