2. Triangles and congruence of triangles 2.1. Basic measurements
... In the following few exercises, when you are asked to prove something you may assume that AAS, ASA, SAS and SSS are true. One other fact that you may use is Thm. 3.4: the sum of the angles of a triangle is π. Note that this is only for these exercises; in general we cannot assume things we have not ...
... In the following few exercises, when you are asked to prove something you may assume that AAS, ASA, SAS and SSS are true. One other fact that you may use is Thm. 3.4: the sum of the angles of a triangle is π. Note that this is only for these exercises; in general we cannot assume things we have not ...
Warm-Up Exercises
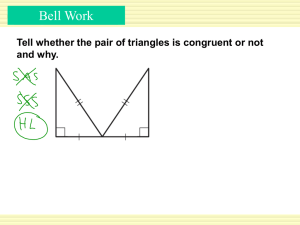
... Can the triangles be proven congruent with the information given in the diagram? If so, state the postulate or theorem you would use. ...
... Can the triangles be proven congruent with the information given in the diagram? If so, state the postulate or theorem you would use. ...
Ch 3 Perpendicular and Parallel Lines
... Statements 1) m 7 = 125°; m 8 = 55° 2) m 7 + m 8 = 125° + m 8 3) m 7 + m 8 = 125° + 55° 4) m 7 + m 8 = 180° 5) 7 & 8 are supplementary 6) j || k ...
... Statements 1) m 7 = 125°; m 8 = 55° 2) m 7 + m 8 = 125° + m 8 3) m 7 + m 8 = 125° + 55° 4) m 7 + m 8 = 180° 5) 7 & 8 are supplementary 6) j || k ...
Postulate 16 Corresponding Angles Converse If 2 lines are cut by a
... Statements 1) m 7 = 125°; m 8 = 55° 2) m 7 + m 8 = 125° + m 8 3) m 7 + m 8 = 125° + 55° 4) m 7 + m 8 = 180° 5) 7 & 8 are supplementary 6) j || k ...
... Statements 1) m 7 = 125°; m 8 = 55° 2) m 7 + m 8 = 125° + m 8 3) m 7 + m 8 = 125° + 55° 4) m 7 + m 8 = 180° 5) 7 & 8 are supplementary 6) j || k ...
Outline of section 4
... Formal basis of quantum mechanics This section puts quantum mechanics onto a more formal mathematical footing by specifying those postulates of the theory which cannot be derived from classical physics. Main ingredients: 1. The wave function (to represent the state of the system) ...
... Formal basis of quantum mechanics This section puts quantum mechanics onto a more formal mathematical footing by specifying those postulates of the theory which cannot be derived from classical physics. Main ingredients: 1. The wave function (to represent the state of the system) ...
The Dot Product of Two Vectors
... 10.1 The Dot and Cross Products of Vectors In this chapter, we shall use two terms which are actually simple. They are scalar field and vector field. We shall not give formal mathematical definitions of these two terms. Consider a mountainous terrain. At every point characterized by x y and z, there ...
... 10.1 The Dot and Cross Products of Vectors In this chapter, we shall use two terms which are actually simple. They are scalar field and vector field. We shall not give formal mathematical definitions of these two terms. Consider a mountainous terrain. At every point characterized by x y and z, there ...
The Thomas-Fermi Theory of Atoms, Molecules and
... grant MPS 71-03375 A03. by the U.S. NSF. under ...
... grant MPS 71-03375 A03. by the U.S. NSF. under ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.