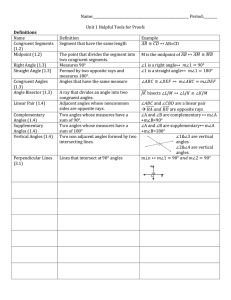
List of all Theorems Def. Postulates grouped by topic.
... Theorem 2.3.7: If two coplanar (does not have to be coplanar lines) lines are each perpendicular to a third line, then these lines are parallel to each other. Postulate 10: (parallel postulate): Through a point not on a line exactly one line is parallel to the given line. ...
... Theorem 2.3.7: If two coplanar (does not have to be coplanar lines) lines are each perpendicular to a third line, then these lines are parallel to each other. Postulate 10: (parallel postulate): Through a point not on a line exactly one line is parallel to the given line. ...
Triangle Similarity: AA, SSS, SAS
... Applying Properties of Similar Triangles Fill in the blanks to complete each theorem. 1. If a line parallel to a side of a triangle intersects the other two sides, then it divides those sides ____________________. 2. If three or more parallel lines intersect two transversals, then they divide the __ ...
... Applying Properties of Similar Triangles Fill in the blanks to complete each theorem. 1. If a line parallel to a side of a triangle intersects the other two sides, then it divides those sides ____________________. 2. If three or more parallel lines intersect two transversals, then they divide the __ ...
Effective Field Theories for Topological states of Matter
... in some simple cases they are known to be ground states of a model Hamiltonian. In the last section, I will briefly describe one important approach based on conformal field theory. The methods just mentioned are all describing the microscopic physics, but there are complementary approaches based on ...
... in some simple cases they are known to be ground states of a model Hamiltonian. In the last section, I will briefly describe one important approach based on conformal field theory. The methods just mentioned are all describing the microscopic physics, but there are complementary approaches based on ...
Curriki Geometry Glossary
... Any of the four angles formed between two straight lines intersected by a third straight line (see also exterior angle) The probability that events A and B both will occur A transformation that is invariant with respect to distance. That is, the distance between any two points in the pre-image must ...
... Any of the four angles formed between two straight lines intersected by a third straight line (see also exterior angle) The probability that events A and B both will occur A transformation that is invariant with respect to distance. That is, the distance between any two points in the pre-image must ...
KVS TGT syllabus
... To skim and scam for specific and general information from a given text/s and read between the lines. To deduce the meaning of unfamiliar lexical items in a given text and provide synonyms / antonyms etc. To organize thoughts coherently in a piece of writing using a variety of cohesive devices. To w ...
... To skim and scam for specific and general information from a given text/s and read between the lines. To deduce the meaning of unfamiliar lexical items in a given text and provide synonyms / antonyms etc. To organize thoughts coherently in a piece of writing using a variety of cohesive devices. To w ...
ch 5 - Ani and Skye-2012
... Theorem 5-4 (OSC ): If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Theorem 5-5(One Pair CP ): If one pair of opposite sides of a quadrilateral are both congruent and parallel, then the quadrilateral is a parallelogram. Theorem 5-6(OAC ): ...
... Theorem 5-4 (OSC ): If both pairs of opposite sides of a quadrilateral are congruent, then the quadrilateral is a parallelogram. Theorem 5-5(One Pair CP ): If one pair of opposite sides of a quadrilateral are both congruent and parallel, then the quadrilateral is a parallelogram. Theorem 5-6(OAC ): ...
Chapter 4 Notes
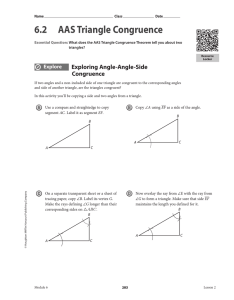
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
... Postulate - ASA – If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the two triangles are congruent. Theorem - AAS – If two angles and a nonincluded side of one triangle are congruent to the corresponding ...
Chapter 6 Power Point Slides File
... Kite -> a quadrilateral with two pairs of adjacent sides congruent and no opposite sides congruent Trapezoid -> a quadrilateral with exactly one pair of parallel sides Isosceles Trapezoid -> a trapezoid whose nonparallel opposite sides are congruent ...
... Kite -> a quadrilateral with two pairs of adjacent sides congruent and no opposite sides congruent Trapezoid -> a quadrilateral with exactly one pair of parallel sides Isosceles Trapezoid -> a trapezoid whose nonparallel opposite sides are congruent ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.