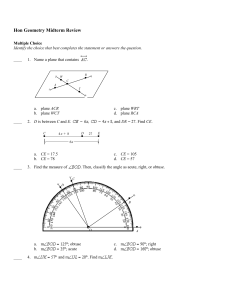
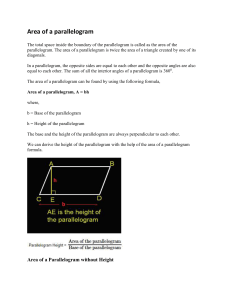
CHAPTER 4 Triangles and Congruence
... Interior Angles (in polygons): The angles inside a closed figure whose sides are line segments. Vertex: The point at which the sides of a polygon intersect. ...
... Interior Angles (in polygons): The angles inside a closed figure whose sides are line segments. Vertex: The point at which the sides of a polygon intersect. ...
Ph125: Quantum Mechanics
... The state of a particle is represented by a vector |ψ(t) i in a Hilbert space. What do we mean by this? We shall define Hilbert space and vectors therein rigorously later; it suffices to say for now that a vector in a Hilbert space is a far more complicated thing than the two numbers x and p that wo ...
... The state of a particle is represented by a vector |ψ(t) i in a Hilbert space. What do we mean by this? We shall define Hilbert space and vectors therein rigorously later; it suffices to say for now that a vector in a Hilbert space is a far more complicated thing than the two numbers x and p that wo ...
9 . 5 Properties and Conditions for Kites and Trapezoids
... In the kite ABCD you constructed in Steps D–F, look at ∠CDE and ∠ADE. What do you notice? _ Is this true for ∠CBE and ∠ABE as well? How can you state this in terms of diagonal AC and the pair of non-congruent opposite angles ∠CBA and ∠CDA? ...
... In the kite ABCD you constructed in Steps D–F, look at ∠CDE and ∠ADE. What do you notice? _ Is this true for ∠CBE and ∠ABE as well? How can you state this in terms of diagonal AC and the pair of non-congruent opposite angles ∠CBA and ∠CDA? ...
Quark models in physics of strong interactions: from the MIT bag to
... Pentaquarks Color Nucleon wave functions p and n magnetic moments Meson wave functions ...
... Pentaquarks Color Nucleon wave functions p and n magnetic moments Meson wave functions ...
Chapter 3
... angle with the 133° angle, they are supplementary by the Consecutive Interior Angles Theorem (Thm. 3.4). The vertical angle is also 133° by the Vertical Angels Congruence Theorem (Thm. 2.6). Because the 133° angle and ∠2 are alternate interior angles, they are congruent by the Alternate Interior Ang ...
... angle with the 133° angle, they are supplementary by the Consecutive Interior Angles Theorem (Thm. 3.4). The vertical angle is also 133° by the Vertical Angels Congruence Theorem (Thm. 2.6). Because the 133° angle and ∠2 are alternate interior angles, they are congruent by the Alternate Interior Ang ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.