Rose-Venus Yousif Intro to 21st Tech. Week 3 Objective: Show and
... 4. Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them. 5. Use inform ...
... 4. Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them. 5. Use inform ...
SU(3) Multiplets & Gauge Invariance
... another possible set of fundamental states carrying the minimum quanta of isospin and hypercharge, though now the eigenvalues (the diagonal elements of 3 and 8) ...
... another possible set of fundamental states carrying the minimum quanta of isospin and hypercharge, though now the eigenvalues (the diagonal elements of 3 and 8) ...
M 333 L Fall 2002 Solutions to Homework #2
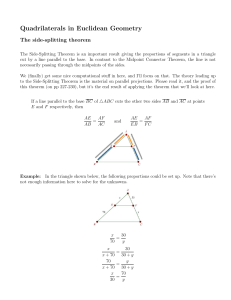
... 5. In proving the converse, you must also divide the proof into two cases: Case 1, which assumes that P is on line segment AB (and thus is the midpoint of line segment AB ) and Case 2, which assumes that P is not on the line segment AB (and so some other point, say M, is the midpoint of line segment ...
... 5. In proving the converse, you must also divide the proof into two cases: Case 1, which assumes that P is on line segment AB (and thus is the midpoint of line segment AB ) and Case 2, which assumes that P is not on the line segment AB (and so some other point, say M, is the midpoint of line segment ...
Exam
... 8. (8) Given a rank-2 tensor T and a vector u, find the transformation rule (in terms of an orthogonal coordinate transform matrix L) for an object w defined through a matrix product expression w = TT u (i.e. w i = TTi ku k) Is w a vector? 9. (10) Calculate the tensor of inertia of a sphere with rad ...
... 8. (8) Given a rank-2 tensor T and a vector u, find the transformation rule (in terms of an orthogonal coordinate transform matrix L) for an object w defined through a matrix product expression w = TT u (i.e. w i = TTi ku k) Is w a vector? 9. (10) Calculate the tensor of inertia of a sphere with rad ...
Geometry Theorems Sheet
... Geometry Theorems Sheet ANY time you are asked to calculate a missing angle or side you must give the reasoning. Here are some short forms. Add to the list as we go through the unit. ...
... Geometry Theorems Sheet ANY time you are asked to calculate a missing angle or side you must give the reasoning. Here are some short forms. Add to the list as we go through the unit. ...
PDF
... The AA theorem may be regarded as the definition of the similarity of triangles. In some texts, the AA theorem is assumed as a postulate. The other two theorems may be proved by using the law of cosines for determining the the ratios other sides (for SAS) and the angles. In hyperbolic geometry and s ...
... The AA theorem may be regarded as the definition of the similarity of triangles. In some texts, the AA theorem is assumed as a postulate. The other two theorems may be proved by using the law of cosines for determining the the ratios other sides (for SAS) and the angles. In hyperbolic geometry and s ...
3/6 Quiz Review with reference sheet and answers File
... corner ® rectangle üï ý Could it be a square? í diagonals ® rhombus ïþ ïî diagonals congruent ...
... corner ® rectangle üï ý Could it be a square? í diagonals ® rhombus ïþ ïî diagonals congruent ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.