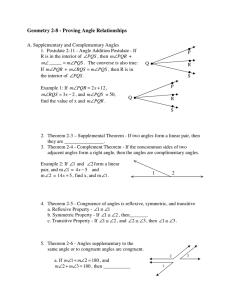
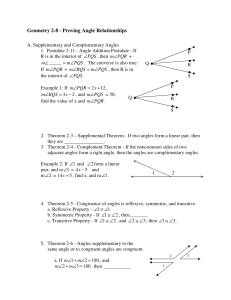
Amrita Engineering Entrance Exam Syllabus 2012
... logarithmic functions. Integration by substitution, by parts and by partial fractions. Integration using trigonometric identities. Integral as a limit of sum. Properties of definite integrals. Evaluation of definite integral; Determining areas of the regions bounded by simple curves. n. Differentia ...
... logarithmic functions. Integration by substitution, by parts and by partial fractions. Integration using trigonometric identities. Integral as a limit of sum. Properties of definite integrals. Evaluation of definite integral; Determining areas of the regions bounded by simple curves. n. Differentia ...
divergence theorem
... It would be extremely difficult to evaluate the given surface integral directly. We would have to evaluate four surface integrals corresponding to the four pieces of S. Also, the divergence of F is much less complicated than F itself: ...
... It would be extremely difficult to evaluate the given surface integral directly. We would have to evaluate four surface integrals corresponding to the four pieces of S. Also, the divergence of F is much less complicated than F itself: ...
Chapter 5: Relationships Within Triangles
... larger corners. Which corners have the larger angles? A ...
... larger corners. Which corners have the larger angles? A ...
Impulse and Momentum
... If hail fell instead of rain, would the force be smaller than, equal to, or greater than that calculated in Example 2? ...
... If hail fell instead of rain, would the force be smaller than, equal to, or greater than that calculated in Example 2? ...
Eureka Math Parent Guide (8th Grade)
... software to understand congruence and similarity. • Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates. • Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence o ...
... software to understand congruence and similarity. • Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates. • Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence o ...
Geometry. “Direct” and “Inverse” Theorems. Ceva`s
... divides the opposite side into parts proportional to the adjacent sides, ...
... divides the opposite side into parts proportional to the adjacent sides, ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.