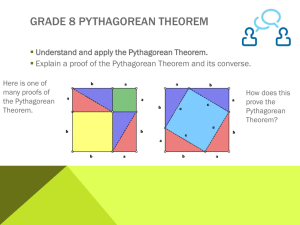
16 The Side-Angle
... fact next example will show that AC need not Suppose that we are given 4ABC and a ray be congruent to DF. ...
... fact next example will show that AC need not Suppose that we are given 4ABC and a ray be congruent to DF. ...
Angular Momentum
... is known then the other two components remain undetermined. This situation is represented by the following diagram: ...
... is known then the other two components remain undetermined. This situation is represented by the following diagram: ...
An equipartition property for high-dimensional log
... This version, and a generalization involving log likelihood ratios with respect to a Markov process, is due independently to Barron [2] and Orey [20]; the definitive version for asymptotically mean stationary processes is due to [2], and Algoet and Cover [1] give an elementary approach to it. The th ...
... This version, and a generalization involving log likelihood ratios with respect to a Markov process, is due independently to Barron [2] and Orey [20]; the definitive version for asymptotically mean stationary processes is due to [2], and Algoet and Cover [1] give an elementary approach to it. The th ...
ExamView - geometry review for final chapters 5 and 6 .tst
... 41. Determine whether each statement is true or false. If true, explain your reasoning. If false, give a ...
... 41. Determine whether each statement is true or false. If true, explain your reasoning. If false, give a ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.