TEAL
... A “ray” is defined parametrically by the equation p (t ) = s + d t p(t) where p(t) is a point on the line at "time" t, s is the starting point, and d is the direction vector of the ray (that is d is a unit vector in the direction of the ray). Thus our “time” t must have dimensions of distance. For e ...
... A “ray” is defined parametrically by the equation p (t ) = s + d t p(t) where p(t) is a point on the line at "time" t, s is the starting point, and d is the direction vector of the ray (that is d is a unit vector in the direction of the ray). Thus our “time” t must have dimensions of distance. For e ...
Triangles - pcrest3.com
... These are not right triangles, so we cannot use the Pythagorean Theorem to find missing side lengths. However, we already have equivalent sides of 1.8 and equivalent angles of 52°. If we can solve for the missing angle (∠x) in triangle 2 and it is equal to 80°, then we can show A-S-A congruency. ∠x ...
... These are not right triangles, so we cannot use the Pythagorean Theorem to find missing side lengths. However, we already have equivalent sides of 1.8 and equivalent angles of 52°. If we can solve for the missing angle (∠x) in triangle 2 and it is equal to 80°, then we can show A-S-A congruency. ∠x ...
subject
... Theorem: Side-Angle-Side Similarity (SAS) Theorem If an angle of one triangle is congruent to an angle of a second triangle, and the sides including the two angles are proportional, then the triangles are similar. B ...
... Theorem: Side-Angle-Side Similarity (SAS) Theorem If an angle of one triangle is congruent to an angle of a second triangle, and the sides including the two angles are proportional, then the triangles are similar. B ...
The AdS 3/CFT2 correspondence in black hole physics
... included, the requirement of preservation of T-duality leads to the presence of the so-called Dbranes, spatially extended objects of any dimension on which open strings can end. It turned out that in any given string theory D-branes can only be stable if their dimensionality is the one dictated by t ...
... included, the requirement of preservation of T-duality leads to the presence of the so-called Dbranes, spatially extended objects of any dimension on which open strings can end. It turned out that in any given string theory D-branes can only be stable if their dimensionality is the one dictated by t ...
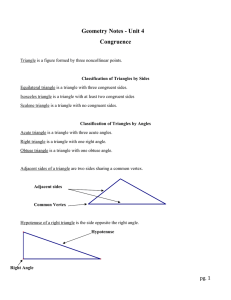
geo meaning earth and metry meaning measures
... For example I can say 2 + 1 = 3 because the definition of the integers tells me that if I add one I get to the next integer. Most things are not so easy to prove and we will be seeing a lot of theorems in this class and we will be proving many of them. Chapter 1-2 Points, Lines, and Planes Point – ...
... For example I can say 2 + 1 = 3 because the definition of the integers tells me that if I add one I get to the next integer. Most things are not so easy to prove and we will be seeing a lot of theorems in this class and we will be proving many of them. Chapter 1-2 Points, Lines, and Planes Point – ...
Boundary-value Problems in Electrostatics I
... In this chapter we shall solve a variety of boundary value problems using techniques which can be described as commonplace. ...
... In this chapter we shall solve a variety of boundary value problems using techniques which can be described as commonplace. ...
RADIATION REACTION AND SELF-FORCE IN CURVED SPACETIME IN A FIELD THEORY APPROACH
... motion of relativistic particles and compact objects in an arbitrary curved spacetime from a field theory approach and depicts the quantum and stochastic (part I), semiclassical (parts I and II), and completely classical regimes (part III). In the semiclassical limit of an open quantum system descri ...
... motion of relativistic particles and compact objects in an arbitrary curved spacetime from a field theory approach and depicts the quantum and stochastic (part I), semiclassical (parts I and II), and completely classical regimes (part III). In the semiclassical limit of an open quantum system descri ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.