4 - Mira Costa High School
... Checkpoint In the diagram, AB , CD , and EF pass through the center M of the ...
... Checkpoint In the diagram, AB , CD , and EF pass through the center M of the ...
An introduction to the Lorentz
... which can always be introduced at a later stage. The parameter ǫ is equal to +1 for the retarded solution, and to −1 for the advanced solution. For the time being we leave j α arbitrary; it could describe an extended charge distribution. We assume that this charge distribution moves slowly: Let rc b ...
... which can always be introduced at a later stage. The parameter ǫ is equal to +1 for the retarded solution, and to −1 for the advanced solution. For the time being we leave j α arbitrary; it could describe an extended charge distribution. We assume that this charge distribution moves slowly: Let rc b ...
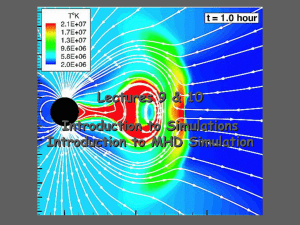
Introduction to simulations
... • The biggest drawback of this approach is that you frequently have to invert very big matrices to solve the linear equations. • Some modern approaches combine implicit and explicit approaches. (The solar code used for the flux cancellation model is semi-implicit.) • The two MHD codes we will use in ...
... • The biggest drawback of this approach is that you frequently have to invert very big matrices to solve the linear equations. • Some modern approaches combine implicit and explicit approaches. (The solar code used for the flux cancellation model is semi-implicit.) • The two MHD codes we will use in ...
4.5 Notes
... tower B, and the fire form a triangle. The dispatcher knows the distance from tower A to tower B and the measures of A and B. So, the measures of two angles and an included side of the triangle are known. By the ASA Congruence Postulate, all triangles with these measures are congruent. So, the trian ...
... tower B, and the fire form a triangle. The dispatcher knows the distance from tower A to tower B and the measures of A and B. So, the measures of two angles and an included side of the triangle are known. By the ASA Congruence Postulate, all triangles with these measures are congruent. So, the trian ...
Pre-AP Geometry – Chapter 5 Test Review
... D.2.a.: I can identify and classify triangles by their sides and angles. D.2.j. I can apply the Isosceles Triangle Theorem and its converse to triangles to solve mathematical and real-world problems. G.CO.8.: I can understand the idea of a rigid motion in the context of triangle congruence. ...
... D.2.a.: I can identify and classify triangles by their sides and angles. D.2.j. I can apply the Isosceles Triangle Theorem and its converse to triangles to solve mathematical and real-world problems. G.CO.8.: I can understand the idea of a rigid motion in the context of triangle congruence. ...
Noether's theorem

Noether's (first) theorem states that every differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proven by German mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function (which may or may not be an integral over space of a Lagrangian density function), from which the system's behavior can be determined by the principle of least action.Noether's theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalization of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (developed in 1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian alone (e.g. systems with a Rayleigh dissipation function). In particular, dissipative systems with continuous symmetries need not have a corresponding conservation law.