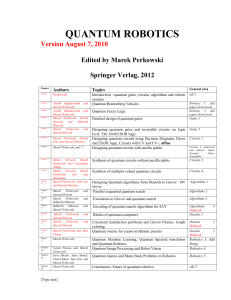
Algebraic graph theory
... Cayley Graphs Groups can also be used to construct graphs. Pick a group G and a subset S (closed under inverses). Define a graph with vertex set G , and “edge set” S, denoted by Cay(G , S). ...
... Cayley Graphs Groups can also be used to construct graphs. Pick a group G and a subset S (closed under inverses). Define a graph with vertex set G , and “edge set” S, denoted by Cay(G , S). ...
Chapter 1
... Sphere. The basis states |0 and |1 are just two points on the Bloch Sphere. Superposition is of the form |0 + |1 where and are complex numbers called quantum amplitudes. These values and are so constrained that they correspond to all points on the surface of the sphere. It can be showe ...
... Sphere. The basis states |0 and |1 are just two points on the Bloch Sphere. Superposition is of the form |0 + |1 where and are complex numbers called quantum amplitudes. These values and are so constrained that they correspond to all points on the surface of the sphere. It can be showe ...
9691 KB pdf file
... Ns and Nt are the number of sites in the spatial and temporal directions respectively. Quark fields are defined on the sites, while the gauge fields are defined as SU(3) matrix valued fields on the links joining the sites. Describing the fermions on the lattice is complicated by the fermion doubling ...
... Ns and Nt are the number of sites in the spatial and temporal directions respectively. Quark fields are defined on the sites, while the gauge fields are defined as SU(3) matrix valued fields on the links joining the sites. Describing the fermions on the lattice is complicated by the fermion doubling ...
Nonlinear Dynamics - CAMTP
... ideas, results and motivations are brilliant and were very influential worldwide over past four decades, although not yet sufficiently well recognized. He has educated a number of excellent younger scientists who now work at universities worldwide, and was also associated with our schools and confer ...
... ideas, results and motivations are brilliant and were very influential worldwide over past four decades, although not yet sufficiently well recognized. He has educated a number of excellent younger scientists who now work at universities worldwide, and was also associated with our schools and confer ...
Quantum Computing - Department of Computing
... Quantum mechanics is a very accurate description of nature as it predicts quantum effects up to an astonishing precision of 14 decimal places. But we do not know why nature works like that and why quantum mechanics gives such a good description of nature. In other words, quantum mechanics tells us h ...
... Quantum mechanics is a very accurate description of nature as it predicts quantum effects up to an astonishing precision of 14 decimal places. But we do not know why nature works like that and why quantum mechanics gives such a good description of nature. In other words, quantum mechanics tells us h ...
Quantum Computing
... Basic quantum information ideas are next outlined, including qubits and data compression, quantum gates, the ‘no cloning’ property, and teleportation. Quantum cryptography is briefly sketched. The universal quantum computer is described, based on the Church-Turing Principle and a network model of co ...
... Basic quantum information ideas are next outlined, including qubits and data compression, quantum gates, the ‘no cloning’ property, and teleportation. Quantum cryptography is briefly sketched. The universal quantum computer is described, based on the Church-Turing Principle and a network model of co ...
Quantum Transport in Finite Disordered Electron Systems
... In Part II an atomic-scale quantum point contact was studied with the intention to investigate the effect of the attached leads on its conductance (i.e., the effect of “measuring apparatus” on the “result of measurement”, in the sense of quantum measurement theory). The practical merit of this study i ...
... In Part II an atomic-scale quantum point contact was studied with the intention to investigate the effect of the attached leads on its conductance (i.e., the effect of “measuring apparatus” on the “result of measurement”, in the sense of quantum measurement theory). The practical merit of this study i ...
4a.pdf
... hyperbolic structure on M itself is that its developing map, in a neighborhood of each edge, should come from a local homeomorphism of M itself. In particular, the sum of the dihedral angles of the edges e1 , . . . , ek must be 2π. Even when this condition is satisfied, though, the holonomy going ar ...
... hyperbolic structure on M itself is that its developing map, in a neighborhood of each edge, should come from a local homeomorphism of M itself. In particular, the sum of the dihedral angles of the edges e1 , . . . , ek must be 2π. Even when this condition is satisfied, though, the holonomy going ar ...
23 - Electronic Colloquium on Computational Complexity
... This transformation takes any state and rotates it by Θ counterclockwise. Fix Θ = π/4. Then it’s clear from the picture that if we were to apply UΘ to |0i, we’d get |+i. If we were to apply UΘ one more time, then we’d get |1i. This small example illustrates what’s called interference: the central ph ...
... This transformation takes any state and rotates it by Θ counterclockwise. Fix Θ = π/4. Then it’s clear from the picture that if we were to apply UΘ to |0i, we’d get |+i. If we were to apply UΘ one more time, then we’d get |1i. This small example illustrates what’s called interference: the central ph ...
Confusions about fuzzballs and the information paradox
... circles in the geometry, and the circles fiber nontrivially over the noncompact direction to make a KK monopole structure. We actually get this KK monopole tensored with a S 1 in the noncompact directions, so that the overall KK charge is zero; thus we call it a ‘dipole charge’. Different shapes of ...
... circles in the geometry, and the circles fiber nontrivially over the noncompact direction to make a KK monopole structure. We actually get this KK monopole tensored with a S 1 in the noncompact directions, so that the overall KK charge is zero; thus we call it a ‘dipole charge’. Different shapes of ...
Topological phases and polaron physics in ultra cold quantum gases
... R Alternative Check of the RG – Kagan-Prokof ’ev theory R.1 Simplified Model . . . . . . . . . . . . . . . . . . . . . . . . R.2 Relation to Kagan and Prokof’ev theory . . . . . . . . . . . R.2.1 Kagan-Prokof’ev theory . . . . . . . . . . . . . . . . R.2.2 Polaron Hamiltonian . . . . . . . . . . . . ...
... R Alternative Check of the RG – Kagan-Prokof ’ev theory R.1 Simplified Model . . . . . . . . . . . . . . . . . . . . . . . . R.2 Relation to Kagan and Prokof’ev theory . . . . . . . . . . . R.2.1 Kagan-Prokof’ev theory . . . . . . . . . . . . . . . . R.2.2 Polaron Hamiltonian . . . . . . . . . . . . ...
URL - StealthSkater
... real numbers, it might be possible to generalize the residue formula. One can also imagine of extending residue calculus to any algebraic extension. An interesting situation arises when the poles correspond to extended p-Adic rationals common to different pages of the "Great Book". Could this mean t ...
... real numbers, it might be possible to generalize the residue formula. One can also imagine of extending residue calculus to any algebraic extension. An interesting situation arises when the poles correspond to extended p-Adic rationals common to different pages of the "Great Book". Could this mean t ...