Tyaglov_Fourier_and_Real_Analysis_Syllabus_Form
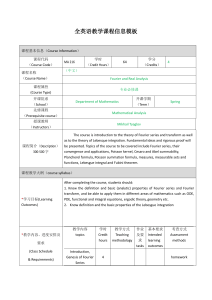
... The course is introduction to the theory of Fourier series and transform as well as to the theory of Lebesque integration. Fundamental ideas and rigorous proof will be presented. Topics of the course to be covered include Fourier series, their convergence and applications, Poisson kernel, Cesaro and ...
... The course is introduction to the theory of Fourier series and transform as well as to the theory of Lebesque integration. Fundamental ideas and rigorous proof will be presented. Topics of the course to be covered include Fourier series, their convergence and applications, Poisson kernel, Cesaro and ...
1 - Cheriton School of Computer Science
... [Shor ’94]: polynomial-time algorithm for factoring integers on a quantum computer This could be used to break most of the existing public-key cryptosystems, including RSA, and elliptic curve crypto [Bennett, Brassard ’84]: provably secure codes with short keys ...
... [Shor ’94]: polynomial-time algorithm for factoring integers on a quantum computer This could be used to break most of the existing public-key cryptosystems, including RSA, and elliptic curve crypto [Bennett, Brassard ’84]: provably secure codes with short keys ...
Quantum dynamics - Psychological Sciences
... • Non-commutative with other operators • Simple in geometric space, but more difficult to construct for higher-dimensional spaces we’ll be using – E.g. for response times – Or for probability judgments (0, 10, 20, …, 100%) – Or for preferences on a Likert scale (1, 2, 3, …, 9) ...
... • Non-commutative with other operators • Simple in geometric space, but more difficult to construct for higher-dimensional spaces we’ll be using – E.g. for response times – Or for probability judgments (0, 10, 20, …, 100%) – Or for preferences on a Likert scale (1, 2, 3, …, 9) ...
1 - the David R. Cheriton School of Computer Science
... [Shor ’94]: polynomial-time algorithm for factoring integers on a quantum computer This could be used to break most of the existing public-key cryptosystems, including RSA, and elliptic curve crypto [Bennett, Brassard ’84]: provably secure codes with short keys ...
... [Shor ’94]: polynomial-time algorithm for factoring integers on a quantum computer This could be used to break most of the existing public-key cryptosystems, including RSA, and elliptic curve crypto [Bennett, Brassard ’84]: provably secure codes with short keys ...
Particles in a Quantum Ontology of Properties
... 1978), use them; an ontology populated by individual objects is thus universally presupposed. The appropriate background theory for all these logics is set theory: ‘ a A ’ expresses that the element ‘a’ belongs to the set of individuals represented by ‘A’. In short, it is a universal and basic cha ...
... 1978), use them; an ontology populated by individual objects is thus universally presupposed. The appropriate background theory for all these logics is set theory: ‘ a A ’ expresses that the element ‘a’ belongs to the set of individuals represented by ‘A’. In short, it is a universal and basic cha ...
Working Group "Young DPG" Arbeitsgruppe junge DPG (AGjDPG
... AGjDPG 1: Tutorial: From spin models to macroeconomics (SOE, DY, jDPG) Formulated as a minimal model of ferromagnets, the Lenz-Ising model received a recent renaissance serving as paradigmatic basis for the formulation and analysis of models of social and economic behaviour. Prominent examples are m ...
... AGjDPG 1: Tutorial: From spin models to macroeconomics (SOE, DY, jDPG) Formulated as a minimal model of ferromagnets, the Lenz-Ising model received a recent renaissance serving as paradigmatic basis for the formulation and analysis of models of social and economic behaviour. Prominent examples are m ...
NEW COVER SLIDE- qinfo with p & a
... A measurement of a two-state system can only yield two possible results. If the measurement isn't guaranteed to succeed, there are three possible results: (1), (2), and ("I don't know"). Therefore, to discriminate between two non-orth. states, we need to use an expanded (3D or more) system. To disti ...
... A measurement of a two-state system can only yield two possible results. If the measurement isn't guaranteed to succeed, there are three possible results: (1), (2), and ("I don't know"). Therefore, to discriminate between two non-orth. states, we need to use an expanded (3D or more) system. To disti ...
Interaction-induced Lipkin-Meshkov-Glick model in a Bose
... collective spin system with long-rang interactions. By changing the effective magnetic field, this model has a rich phase diagram in both ground- and excited- states, independent of the systemsize [6, 7, 8, 9, 10, 11]. In quantum information it can be used to test the fundamental relation between ma ...
... collective spin system with long-rang interactions. By changing the effective magnetic field, this model has a rich phase diagram in both ground- and excited- states, independent of the systemsize [6, 7, 8, 9, 10, 11]. In quantum information it can be used to test the fundamental relation between ma ...
Localization in discontinuous quantum systems
... discontinuous, periodic and bounded (|f (θ)| ≤ 1) functions. This set of functions can be also enlarged to continuous bounded functions with a discontinuous derivative. In this case the situation is slightly complicated, since usually a critical value of the parameter K = kT appears (see [6] for the ...
... discontinuous, periodic and bounded (|f (θ)| ≤ 1) functions. This set of functions can be also enlarged to continuous bounded functions with a discontinuous derivative. In this case the situation is slightly complicated, since usually a critical value of the parameter K = kT appears (see [6] for the ...
LECTURES ON SYMPLECTIC REFLECTION ALGEBRAS Setting. W
... an isomorphism. Then we prove that the natural morphism RepΓ (H0,c , CΓ)// GL(CΓ)Γ → Spec(eH0,c e) is an isomorphism. Let y1 , . . . , yn be the tautological basis in Cn = h and x1 , . . . , xn be the dual basis in h∗ . The elements xn , yn still act on N Sn−1 ∼ = Cn . Show that [xn , yn ] ∈ O = {A| ...
... an isomorphism. Then we prove that the natural morphism RepΓ (H0,c , CΓ)// GL(CΓ)Γ → Spec(eH0,c e) is an isomorphism. Let y1 , . . . , yn be the tautological basis in Cn = h and x1 , . . . , xn be the dual basis in h∗ . The elements xn , yn still act on N Sn−1 ∼ = Cn . Show that [xn , yn ] ∈ O = {A| ...
A DIRECT PROOF OF THE QUANTUM VERSION OF MONK`S
... degeneracy loci formulas on hyper-quot schemes. In the present paper we give a direct geometric proof of the quantum Monk’s formula which relies only on classical Schubert calculus and the definition of Gromov-Witten invariants. In particular, no compactifications of moduli spaces are required. Our ...
... degeneracy loci formulas on hyper-quot schemes. In the present paper we give a direct geometric proof of the quantum Monk’s formula which relies only on classical Schubert calculus and the definition of Gromov-Witten invariants. In particular, no compactifications of moduli spaces are required. Our ...
A quantum-information-theoretic complement to a general
... A model in GR is a triple hM, gab , Tab i such that the Einstein field equations are satisfied, where M is a four-dimensional Lorentzian manifold, gab the metric tensor, and Tab the energy-momentum tensor. An ordered pair hM, gab i such that there exists a Tab for which the triple hM, gab , Tab i is ...
... A model in GR is a triple hM, gab , Tab i such that the Einstein field equations are satisfied, where M is a four-dimensional Lorentzian manifold, gab the metric tensor, and Tab the energy-momentum tensor. An ordered pair hM, gab i such that there exists a Tab for which the triple hM, gab , Tab i is ...
The Problem of Confirmation in the Everett Interpretation
... One of the most striking features of quantum theory is that systems can be in superpositions of states normally thought to be mutually exclusive. Moreoever, the time-dependent Schrodinger’s equation implies that quantum systems undergo linear, deterministic evolution. This means that in any measurem ...
... One of the most striking features of quantum theory is that systems can be in superpositions of states normally thought to be mutually exclusive. Moreoever, the time-dependent Schrodinger’s equation implies that quantum systems undergo linear, deterministic evolution. This means that in any measurem ...
Quantum Information and Quantum Computation
... Chapter 43. Quantum Information and Quantum Computation Researchers at the W.M. Keck Center for Extreme Quantum Information Theory (xQIT) are Working to investigate the limits of computation and communication. We are working to uncover the abilities of quantum computers to solve hard problems. We a ...
... Chapter 43. Quantum Information and Quantum Computation Researchers at the W.M. Keck Center for Extreme Quantum Information Theory (xQIT) are Working to investigate the limits of computation and communication. We are working to uncover the abilities of quantum computers to solve hard problems. We a ...
Quantum Mechanics of the Solar System - Latin
... tools of Schrödinger’s wave mechanics and we discuss their interpretation in connection with classical physics. This example could be of real pedagogical interest for students because it covers subjects ranging from classical and quantum mechanics and the theory of perturbations and goes beyond the ...
... tools of Schrödinger’s wave mechanics and we discuss their interpretation in connection with classical physics. This example could be of real pedagogical interest for students because it covers subjects ranging from classical and quantum mechanics and the theory of perturbations and goes beyond the ...























