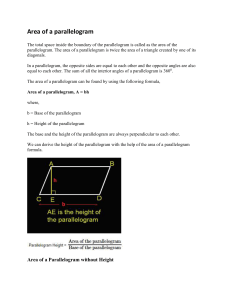
Unit 7 - Georgia Standards
... congruent if and only if their corresponding sides and corresponding angles are congruent • use the definition of congruence, based on rigid motion, to develop and explain the triangle congruence criteria; ASA, SSS, and SAS • prove theorems pertaining to lines and angles • prove theorems pertaining ...
... congruent if and only if their corresponding sides and corresponding angles are congruent • use the definition of congruence, based on rigid motion, to develop and explain the triangle congruence criteria; ASA, SSS, and SAS • prove theorems pertaining to lines and angles • prove theorems pertaining ...

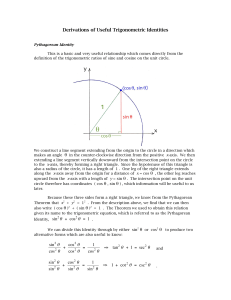















![arXiv:math/0510054v2 [math.HO] 17 Aug 2006](http://s1.studyres.com/store/data/014467696_1-4b3b027c0fc1865fd923af6e7da50abe-300x300.png)