ATM 316 - Augmentation of Newton`s 2nd law for Earth`s rotation
... law applies to this term. The first term on the right hand side (RHS) is what we want, the change ~ seen from Earth. The second RHS term is the rotation of the Earth as seen from space. in A ~ = 0 and Examples: Say the Earth is not rotating (sphericity not being considered yet). Then Ω ...
... law applies to this term. The first term on the right hand side (RHS) is what we want, the change ~ seen from Earth. The second RHS term is the rotation of the Earth as seen from space. in A ~ = 0 and Examples: Say the Earth is not rotating (sphericity not being considered yet). Then Ω ...
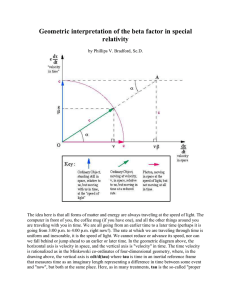
A space-time geometric interpretation of the beta factor in Special
... Hermann Minkowski (1864-1909), a German Professor of mathematics, born in Russia, developed a number system that seems appropriate for describing co-ordinates in a fourdimensional space-time continuum. In his approach, we may think of events in space-time that occur at a particular place and at a p ...
... Hermann Minkowski (1864-1909), a German Professor of mathematics, born in Russia, developed a number system that seems appropriate for describing co-ordinates in a fourdimensional space-time continuum. In his approach, we may think of events in space-time that occur at a particular place and at a p ...
Example 2 Second-Order Chemical reaction
... A differential equation describing the velocity v of a falling object subject to air resistance proportional to the instantaneous velocity is ...
... A differential equation describing the velocity v of a falling object subject to air resistance proportional to the instantaneous velocity is ...
Announcements
... spectrum. To understand this gravitational redshift, think of a baseball hit high into the air, slowing as it climbs. Einstein’s theory says that as a photon fights its way out of a gravitational field, it loses energy and its color reddens. (It can’t lose speed since ...
... spectrum. To understand this gravitational redshift, think of a baseball hit high into the air, slowing as it climbs. Einstein’s theory says that as a photon fights its way out of a gravitational field, it loses energy and its color reddens. (It can’t lose speed since ...
Euler Force
... Thus the time derivative of these vectors, which rotate without changing magnitude, is ...
... Thus the time derivative of these vectors, which rotate without changing magnitude, is ...