2886grading2890 - Emerson Statistics Home
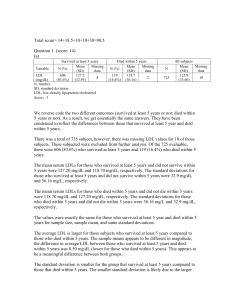
... compared to those who did not die within 5 years. The 95% confidence interval suggests that this observation is not unusual if the true difference in mean LDL lowering for a patient who died within 5 years were between a 1.91 and 15.09 mg/dL decrease. Because the P-value is P=0.012, we reject the nu ...
... compared to those who did not die within 5 years. The 95% confidence interval suggests that this observation is not unusual if the true difference in mean LDL lowering for a patient who died within 5 years were between a 1.91 and 15.09 mg/dL decrease. Because the P-value is P=0.012, we reject the nu ...
Di erence-in-Di erences Inference with Few Treated Clusters ∗
... and Miller (2015) provides a recent and comprehensive survey. While much progress has been made, there are still situations in which reliable inference is a challenge. It is particularly challenging when there are very few treated clusters. Past research, including Conley and Taber (2011), has shown ...
... and Miller (2015) provides a recent and comprehensive survey. While much progress has been made, there are still situations in which reliable inference is a challenge. It is particularly challenging when there are very few treated clusters. Past research, including Conley and Taber (2011), has shown ...
Example
... Mutually Exclusive and Jointly Exhaustive Events A set of events is mutually exclusive if no more than one of the events can occur. A = IBM stock rises by at least $1, B = IBM stock falls by at least $1 A and B are mutually exclusive but not jointly exhaustive A set of events is jointly exhaustiv ...
... Mutually Exclusive and Jointly Exhaustive Events A set of events is mutually exclusive if no more than one of the events can occur. A = IBM stock rises by at least $1, B = IBM stock falls by at least $1 A and B are mutually exclusive but not jointly exhaustive A set of events is jointly exhaustiv ...
Summary of Video
... If a population has the normal distribution with mean µ and standard deviation σ, then the sample mean x of n independent observations has a normal distribution with mean µ and standard deviation σ n . In our example above, the population distribution was not normal (see Figure 22.7). In such cases ...
... If a population has the normal distribution with mean µ and standard deviation σ, then the sample mean x of n independent observations has a normal distribution with mean µ and standard deviation σ n . In our example above, the population distribution was not normal (see Figure 22.7). In such cases ...
Describing Data:
... If we consider only the central value in a set of data, or if we compare several sets of data using central values, we may draw an erroneous conclusion. In addition to the central values, we should consider the dispersion—often called the variation or the spread—in the data. As an illustration, supp ...
... If we consider only the central value in a set of data, or if we compare several sets of data using central values, we may draw an erroneous conclusion. In addition to the central values, we should consider the dispersion—often called the variation or the spread—in the data. As an illustration, supp ...
Package `metRology`
... The metRology package includes functions for: • Plotting for Key Comparisons (dot-and-bar, consistency) • Uncertainty evaluation using algebraic or numeric differentiation, with support for correlation • Monte Carlo evaluation of uncertainty (including correlation for normally distributed variables) ...
... The metRology package includes functions for: • Plotting for Key Comparisons (dot-and-bar, consistency) • Uncertainty evaluation using algebraic or numeric differentiation, with support for correlation • Monte Carlo evaluation of uncertainty (including correlation for normally distributed variables) ...
Inference for means
... The sample mean X̄ as a point estimate of µ Even without using any ideas from probability or distribution theory, it seems compelling that the sample mean should tell us something about the population mean. If we have a random sample from the population, the sample should be representative of the po ...
... The sample mean X̄ as a point estimate of µ Even without using any ideas from probability or distribution theory, it seems compelling that the sample mean should tell us something about the population mean. If we have a random sample from the population, the sample should be representative of the po ...
Non-crossing quantile regression curve estimation
... percentiles (0.25, 0.5, 0.75, 0.9, 0.95, 0.99). The fitted slopes of the quantile functions give the effects of the covariates at the various levels of cyclone intensity. One particular issue with fitting the upper quantiles is the lack of data, hence fitting individual quantile curves can be even m ...
... percentiles (0.25, 0.5, 0.75, 0.9, 0.95, 0.99). The fitted slopes of the quantile functions give the effects of the covariates at the various levels of cyclone intensity. One particular issue with fitting the upper quantiles is the lack of data, hence fitting individual quantile curves can be even m ...