Introduction to Matrix Algebra
... (1− λ )a1 +ρa2 = 0 (1− λ )a2 + ρ a1 = 0 Now take the largest eigenvalue, l = 1 + r, and substitute. This gives ρ( a2 − a1 ) = 0 ρ( a1 − a2 ) = 0 Thus, all we know is that a 1 = a 2 . If we let a 1 = 10, then a 2 = 10; and if we let a 1 = -.023, then a 2 = -.023. This is what was meant above when it ...
... (1− λ )a1 +ρa2 = 0 (1− λ )a2 + ρ a1 = 0 Now take the largest eigenvalue, l = 1 + r, and substitute. This gives ρ( a2 − a1 ) = 0 ρ( a1 − a2 ) = 0 Thus, all we know is that a 1 = a 2 . If we let a 1 = 10, then a 2 = 10; and if we let a 1 = -.023, then a 2 = -.023. This is what was meant above when it ...
1 Facts concerning Hamel bases - East
... choice is also equivalent to the statement, that for every set x there exists an ordinal number α and a bijection f : α → x. The class of all ordinal numbers is transitive and well-ordered by ∈. The set of all natural numbers is equal to the set of all finite ordinal numbers and is denoted by ω. (A n ...
... choice is also equivalent to the statement, that for every set x there exists an ordinal number α and a bijection f : α → x. The class of all ordinal numbers is transitive and well-ordered by ∈. The set of all natural numbers is equal to the set of all finite ordinal numbers and is denoted by ω. (A n ...
41. Feedback--invariant optimal control theory and differential
... ΛV1 with ΛV2 . Hence ΛV1 ≤ ΛV2 in the space of quadratic forms. Remark 1.1 The signs of quadratic forms under consideration and the monotonicity types of curves in the Lagrange Grassmannian depend on the general sign agreement which varies from paper to paper. So ΛV , V ⊃ Vo , form a monotonically i ...
... ΛV1 with ΛV2 . Hence ΛV1 ≤ ΛV2 in the space of quadratic forms. Remark 1.1 The signs of quadratic forms under consideration and the monotonicity types of curves in the Lagrange Grassmannian depend on the general sign agreement which varies from paper to paper. So ΛV , V ⊃ Vo , form a monotonically i ...
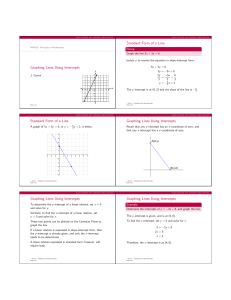
Graphing Lines Using Intercepts
... That is, in the equation 5x − 4y = 20, both 5 and −4 are factors of 20. If the standard form of a line has this relationship between the coefficients and the constant term, then the x- and y -intercepts will turn out to be “nice” integral values. On the other hand, if this relationship is not presen ...
... That is, in the equation 5x − 4y = 20, both 5 and −4 are factors of 20. If the standard form of a line has this relationship between the coefficients and the constant term, then the x- and y -intercepts will turn out to be “nice” integral values. On the other hand, if this relationship is not presen ...
Linear algebra
Linear algebra is the branch of mathematics concerning vector spaces and linear mappings between such spaces. It includes the study of lines, planes, and subspaces, but is also concerned with properties common to all vector spaces.The set of points with coordinates that satisfy a linear equation forms a hyperplane in an n-dimensional space. The conditions under which a set of n hyperplanes intersect in a single point is an important focus of study in linear algebra. Such an investigation is initially motivated by a system of linear equations containing several unknowns. Such equations are naturally represented using the formalism of matrices and vectors.Linear algebra is central to both pure and applied mathematics. For instance, abstract algebra arises by relaxing the axioms of a vector space, leading to a number of generalizations. Functional analysis studies the infinite-dimensional version of the theory of vector spaces. Combined with calculus, linear algebra facilitates the solution of linear systems of differential equations.Techniques from linear algebra are also used in analytic geometry, engineering, physics, natural sciences, computer science, computer animation, and the social sciences (particularly in economics). Because linear algebra is such a well-developed theory, nonlinear mathematical models are sometimes approximated by linear models.