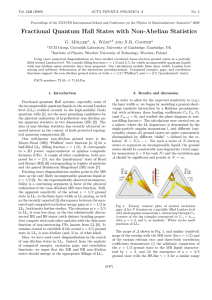
Landau-level distribution of electrons moving with velocities
... one. Thus, there is hope that this system will require an inverted population of the energy levels. However, in this process, the principal role is played by the competition of the radiated anomalous and normal Doppler frequencies. For classical systems, this process was considered earlier by Ginzbu ...
... one. Thus, there is hope that this system will require an inverted population of the energy levels. However, in this process, the principal role is played by the competition of the radiated anomalous and normal Doppler frequencies. For classical systems, this process was considered earlier by Ginzbu ...
week_10_homework_kinetic_and_potential_energy
... On the axes below sketch a graph showing how the passenger’s gravitational potential energy would vary with time as he ascended from A to C. Add a scale to each axis. ...
... On the axes below sketch a graph showing how the passenger’s gravitational potential energy would vary with time as he ascended from A to C. Add a scale to each axis. ...
The Photoelectric Effect
... the effect was first discovered, one of the most striking things about it was that it could not be explained by the classical theory of electromagnetism, the only available theory of light at the time. Firstly, we will define a few terms. The electrons emitted from the surface are called photoelectr ...
... the effect was first discovered, one of the most striking things about it was that it could not be explained by the classical theory of electromagnetism, the only available theory of light at the time. Firstly, we will define a few terms. The electrons emitted from the surface are called photoelectr ...
Ch 7
... Existence (and energy) of electron in atom is described by its unique wave function Y. Pauli exclusion principle - no two electrons in an atom can have the same four quantum numbers. ...
... Existence (and energy) of electron in atom is described by its unique wave function Y. Pauli exclusion principle - no two electrons in an atom can have the same four quantum numbers. ...
TOPPER SAMPLE PAPER 4 XI – PHYSICS
... 19. The kinetic energy of a satellite is E. Find the total energy of the satellite. ...
... 19. The kinetic energy of a satellite is E. Find the total energy of the satellite. ...
AP Physics things to remember
... Increasing the intensity of a beam of light can be done in two ways ____________ and __________ Compton Shift both momentum and K are conserved in a collision of a photon and electron. If EMR is shining on a surface but there is not enough energy to knock electrons out because the work function has ...
... Increasing the intensity of a beam of light can be done in two ways ____________ and __________ Compton Shift both momentum and K are conserved in a collision of a photon and electron. If EMR is shining on a surface but there is not enough energy to knock electrons out because the work function has ...
Intro to EMR and Wave Equation
... • The electric field is parallel to the conductor and the magnetic field is perpendicular to the conductor ...
... • The electric field is parallel to the conductor and the magnetic field is perpendicular to the conductor ...
3D Rigid Body Dynamics: Kinetic Energy, Instability, Equations of
... for angular momentum: internal forces and motions will not change angular momentum. The implications of this can be profound. Consider a body spinning about the z axis of inertia with no external moments. Then the angular momentum � G = Hz�k will be will be constant and since it is a vector, it will ...
... for angular momentum: internal forces and motions will not change angular momentum. The implications of this can be profound. Consider a body spinning about the z axis of inertia with no external moments. Then the angular momentum � G = Hz�k will be will be constant and since it is a vector, it will ...








![[2014 solutions]](http://s1.studyres.com/store/data/008881817_1-9b59b3a488861f750cad1da068f01a69-300x300.png)