STAT 155 Introductory Statistics Lecture 13: Birthday Problem
... • In a classroom of 45 people, what is the probability that at least two people have the same birthday? • Event A: at least two people have the same birthday out of the 45 people. • AC: every person has a different birthday out of the 45 people. • P(A) = 1 - P(AC) = … (see the board) ...
... • In a classroom of 45 people, what is the probability that at least two people have the same birthday? • Event A: at least two people have the same birthday out of the 45 people. • AC: every person has a different birthday out of the 45 people. • P(A) = 1 - P(AC) = … (see the board) ...
Paradoxes in Probability Theory
... For r > 12 , it will always make sense (in terms of expected amount received) to switch envelopes upon looking in one. Eckhardt moves quickly from the general problem formulation to analyzing this particular model. I agree with him that the behavior of the model is a bit surprising. Note, however, t ...
... For r > 12 , it will always make sense (in terms of expected amount received) to switch envelopes upon looking in one. Eckhardt moves quickly from the general problem formulation to analyzing this particular model. I agree with him that the behavior of the model is a bit surprising. Note, however, t ...
AP STATISTICS MIDTERM EXAM REVIEW CHAPTER 6 Use the
... 15. To pass the time, a toll booth collector counts the number of cars that pass through his booth until he encounters a driver with red hair. Suppose we define the random variable Y = the number of cars the collector counts until he gets a red-headed driver for the first time. Is Y a geometric rand ...
... 15. To pass the time, a toll booth collector counts the number of cars that pass through his booth until he encounters a driver with red hair. Suppose we define the random variable Y = the number of cars the collector counts until he gets a red-headed driver for the first time. Is Y a geometric rand ...
Probability - Learn Alberta
... Francesca is at the Grande Prairie fair. Her favourite game is the bottle ring toss because of the prizes. Winners at this game can win large stuffed dragons, medium stuffed panda bears, small stuffed zebras, CDs or ride coupons. Assuming she wins every time she plays, what is the probability that F ...
... Francesca is at the Grande Prairie fair. Her favourite game is the bottle ring toss because of the prizes. Winners at this game can win large stuffed dragons, medium stuffed panda bears, small stuffed zebras, CDs or ride coupons. Assuming she wins every time she plays, what is the probability that F ...
ECS 20 Chapter 7, Probability 1. Introduction 1.1. Probability theory
... Random variables can be discrete, e.g. a count of the heads in six flipped coins, or continuous, e.g. the temperature during a day. 7.1.1. Let s ∈ S, then P(x = a) ≡ P({s | X(s) = a}), and P(a ≤ X ≤ b) ≡ P({s | a ≤ X(s) ≤ b}) 7.2. Suppose a discrete random variable X can only take on the values x1, ...
... Random variables can be discrete, e.g. a count of the heads in six flipped coins, or continuous, e.g. the temperature during a day. 7.1.1. Let s ∈ S, then P(x = a) ≡ P({s | X(s) = a}), and P(a ≤ X ≤ b) ≡ P({s | a ≤ X(s) ≤ b}) 7.2. Suppose a discrete random variable X can only take on the values x1, ...
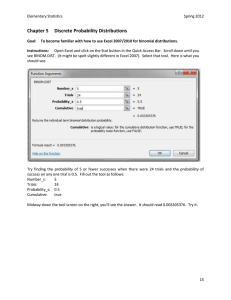
Chapter 5 Discrete Probability Distributions
... by a broadcast method, we would like an even distribution of fertilizer. Too little and growth would be stunted, too much, and it will cause a “burn”. Let’s say that on average, 100 pellets fall on a square meter. What is the probability that 80 pellets or less fall on some square meter? The average ...
... by a broadcast method, we would like an even distribution of fertilizer. Too little and growth would be stunted, too much, and it will cause a “burn”. Let’s say that on average, 100 pellets fall on a square meter. What is the probability that 80 pellets or less fall on some square meter? The average ...
Grade 7 Mathematics Module 5, Topic B, Overview
... then assess the plausibility of the model. In Lessons 10 and 11, students work with simulations. They are either given results from a simulation to approximate a probability (Lesson 10), or they design their own simulation, carry out the simulation, and use the simulation results to approximate a pr ...
... then assess the plausibility of the model. In Lessons 10 and 11, students work with simulations. They are either given results from a simulation to approximate a probability (Lesson 10), or they design their own simulation, carry out the simulation, and use the simulation results to approximate a pr ...