chapter 13 - University of Michigan
... The rigid rotor model assumes that the internuclear distance R is a constant. This is not a bad approximation since the amplitude of vibration is generally of the order of 1% of R. The Schrödinger equation for nuclear motion then involves the three-dimensional angular momentum operator, written Jˆ ...
... The rigid rotor model assumes that the internuclear distance R is a constant. This is not a bad approximation since the amplitude of vibration is generally of the order of 1% of R. The Schrödinger equation for nuclear motion then involves the three-dimensional angular momentum operator, written Jˆ ...
Quantum2
... •We know that the particle’s position cannot be determined precisely, but that the probability of a particle being found at a particular point can be calculated from the wavefunction. •Okay, we can’t calculate the position (or other position dependent variables) precisely but given a large number of ...
... •We know that the particle’s position cannot be determined precisely, but that the probability of a particle being found at a particular point can be calculated from the wavefunction. •Okay, we can’t calculate the position (or other position dependent variables) precisely but given a large number of ...
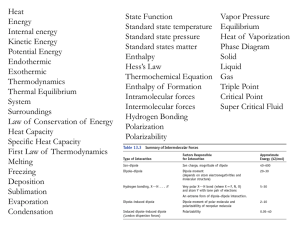
Unit 8 Heat Study Guide A change of state is a ___ Process by
... 1. A change of state is a ___ a. Process by which two states of matter co-exist b. Chemical change c. Physical change that converts a substance from one physical form to another 2. Particles in a __________ move slower than particles in a __________. 3. Particles in a ___ vibrate in place. a. Solid ...
... 1. A change of state is a ___ a. Process by which two states of matter co-exist b. Chemical change c. Physical change that converts a substance from one physical form to another 2. Particles in a __________ move slower than particles in a __________. 3. Particles in a ___ vibrate in place. a. Solid ...
Remarks on Energy in the Many Worlds
... energy. After all, where is all the extra energy, hidden away in those other ever-branching worlds, coming from? A formal answer begins with the observation that in quantum mechanics the energy, like all dynamical quantities, is an operator in Hilbert space, and not a substance in the traditional se ...
... energy. After all, where is all the extra energy, hidden away in those other ever-branching worlds, coming from? A formal answer begins with the observation that in quantum mechanics the energy, like all dynamical quantities, is an operator in Hilbert space, and not a substance in the traditional se ...
Introduction to Quantum Mechanics AEP3610 Professor Scott
... Goals of the course • by speculating on possible analogies between waves moving in a uniform medium and the so-called free particle, to develop some calculational tools for describing matter waves, including the de Broglie wavelength for a moving particle, and the Born interpretion of the wave funct ...
... Goals of the course • by speculating on possible analogies between waves moving in a uniform medium and the so-called free particle, to develop some calculational tools for describing matter waves, including the de Broglie wavelength for a moving particle, and the Born interpretion of the wave funct ...
Some Calculations on the Lithium Atom Ground State
... We now calculate the ground-state energy of lithium assuming it has the 1s 22s1 electronic configuration. The total electronic energy consists of nine contributions: three kinetic energy terms, three electron-nucleus potential energy terms, and three electron-electron potential energy contriubtions. ...
... We now calculate the ground-state energy of lithium assuming it has the 1s 22s1 electronic configuration. The total electronic energy consists of nine contributions: three kinetic energy terms, three electron-nucleus potential energy terms, and three electron-electron potential energy contriubtions. ...
Document
... We have also made the assumption, following Thiemann, that quantum gravity acts as a “fundamental regulator” and therefore delocalized the product of electric fields to two different points tied together by the regulator f We now consider the electric and magnetic fields to be in a coherent states ...
... We have also made the assumption, following Thiemann, that quantum gravity acts as a “fundamental regulator” and therefore delocalized the product of electric fields to two different points tied together by the regulator f We now consider the electric and magnetic fields to be in a coherent states ...
Spontaneous Symmetry Breaking
... N → ∞ at the end of calculations. (There is an important subtlety about one-dimensional quantum systems which actually do not show spontaneous symmetry breaking due to long-range quantum fluctuations. This is known as Mermin–Wagner theorem in condensed matter physics or Coleman’s theorem in 1+1 dime ...
... N → ∞ at the end of calculations. (There is an important subtlety about one-dimensional quantum systems which actually do not show spontaneous symmetry breaking due to long-range quantum fluctuations. This is known as Mermin–Wagner theorem in condensed matter physics or Coleman’s theorem in 1+1 dime ...