X - sibor
... this rule when V is infinite.) In order to normalize the wave functions, they must approach zero as x approaches infinity. ...
... this rule when V is infinite.) In order to normalize the wave functions, they must approach zero as x approaches infinity. ...
The landscape of Anderson localization in a disordered medium
... localization of eigenfunctions remain mysterious. In particular, it seems very difficult to predict where to expect localized vibrations, and for which eigenvalues, without having to solve the full eigenvalue problem. We will address in this paper the case of Anderson localization of quantum states, ...
... localization of eigenfunctions remain mysterious. In particular, it seems very difficult to predict where to expect localized vibrations, and for which eigenvalues, without having to solve the full eigenvalue problem. We will address in this paper the case of Anderson localization of quantum states, ...
Document
... There are three rules which help dictate how electrons are arranged in the atoms. Aufbau Principle- electrons occupy the orbitals of the lowest energy first Hund’s Rule- Orbitals of equal energy are each occupied by one electron before any one orbital is occupied by a second electron. All electrons ...
... There are three rules which help dictate how electrons are arranged in the atoms. Aufbau Principle- electrons occupy the orbitals of the lowest energy first Hund’s Rule- Orbitals of equal energy are each occupied by one electron before any one orbital is occupied by a second electron. All electrons ...
Chapter 5 Electrons in Atoms
... level of an electron • analogous to the rungs of a ladder The electron cannot exist between energy levels, just like you can’t stand between rungs on a ladder A quantum of energy is the amount of energy required to move an electron from one energy level to another ...
... level of an electron • analogous to the rungs of a ladder The electron cannot exist between energy levels, just like you can’t stand between rungs on a ladder A quantum of energy is the amount of energy required to move an electron from one energy level to another ...
Stark effect of the hyperfine structure of ICl in its rovibronic ground
... of |JI 1 F1 I2 F⟩ to obtain the hyperfine levels of J = 0 and 1 rotational states. The molecular constants adopted in the present calculation are listed in Table 1. Note that, C1 is small, which contributes a little to the hyperfine structure, and C2 is so small that it is set to be 0 in our calcula ...
... of |JI 1 F1 I2 F⟩ to obtain the hyperfine levels of J = 0 and 1 rotational states. The molecular constants adopted in the present calculation are listed in Table 1. Note that, C1 is small, which contributes a little to the hyperfine structure, and C2 is so small that it is set to be 0 in our calcula ...
... The new quantum mechanics, when applied to the problem of the structure of the atom with point-charge electrons, does not give results in agreement with experiment. The discrepancies consist of " duplexity " phenomena, the observed number of stationary states for an electron in an atom being twice t ...
Two Body Perturbing Resonances in a Three Body System: Origin of
... There are many missing links in the nuclear structure many body problems, such as the treatment of the repulsive core part of the N-N interaction, inclusion of non-perturbative effects in the many body solution, proper inclusion of tensor interaction, in the field theoretic formulation[1] the necess ...
... There are many missing links in the nuclear structure many body problems, such as the treatment of the repulsive core part of the N-N interaction, inclusion of non-perturbative effects in the many body solution, proper inclusion of tensor interaction, in the field theoretic formulation[1] the necess ...
Electronic Shells of Dirac Fermions in Graphene Quantum Rings in
... There is currently significant interest in graphene based electronics [1–6]. With a single sheet of graphene being a zero-gap semiconductor much effort is directed toward engineering gap in electronic spectrum of graphene by controlling its lateral size and shape [6]. In this approach edges of graph ...
... There is currently significant interest in graphene based electronics [1–6]. With a single sheet of graphene being a zero-gap semiconductor much effort is directed toward engineering gap in electronic spectrum of graphene by controlling its lateral size and shape [6]. In this approach edges of graph ...
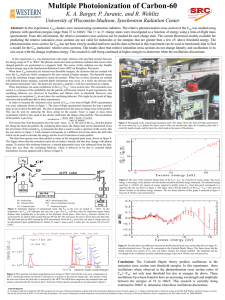
Figure 4 - University of Wisconsin–Madison
... In this experiment, C60 was photoionized with single photons with specified energies between the energy range of 37 to 160eV. The photons used came from synchrotron radiation that occurs when charged particles are accelerated in a magnetic field. The source of this radiation was the Aladdin electron ...
... In this experiment, C60 was photoionized with single photons with specified energies between the energy range of 37 to 160eV. The photons used came from synchrotron radiation that occurs when charged particles are accelerated in a magnetic field. The source of this radiation was the Aladdin electron ...