The classical and quantum mechanics of a particle on a knot.
... that, in the present one-dimensional problem, the role of g is played by [f (φ)]−1 . A straightforward calculation for the Laplace–Beltrami operator using this metric yields the first two terms of the Hamiltonian in (22), but not the third term. This term has its origin in the choice of Weyl orderin ...
... that, in the present one-dimensional problem, the role of g is played by [f (φ)]−1 . A straightforward calculation for the Laplace–Beltrami operator using this metric yields the first two terms of the Hamiltonian in (22), but not the third term. This term has its origin in the choice of Weyl orderin ...
Particle Swarm Optimization by Natural Exponent Inertia Weight for
... The economic load dispatch (ELD) of power generating units has always occupied an important position in the electric power industry. The primary objective of ELD is to schedule the committed generating units output so as to meet the required load demand at minimum cost satisfying all unit and system ...
... The economic load dispatch (ELD) of power generating units has always occupied an important position in the electric power industry. The primary objective of ELD is to schedule the committed generating units output so as to meet the required load demand at minimum cost satisfying all unit and system ...
The strange link between the human mind and quantum physics
... The implication seems to be that each particle passes simultaneously through both slits and interferes with itself. This combination of "both paths at once" is known as a superposition state. But here is the really odd thing. ...
... The implication seems to be that each particle passes simultaneously through both slits and interferes with itself. This combination of "both paths at once" is known as a superposition state. But here is the really odd thing. ...
Full text in PDF form
... Thus, the stability conditions provide a metric in the four-dimensional manifold of spacementropy. The arc length s in the space-mechanical entropy manifold may be parameterized by choosing ds ≡ u0dt ≡ cdt, where u0 ≡ c is the unique velocity appearing in the integrating factor of the second postula ...
... Thus, the stability conditions provide a metric in the four-dimensional manifold of spacementropy. The arc length s in the space-mechanical entropy manifold may be parameterized by choosing ds ≡ u0dt ≡ cdt, where u0 ≡ c is the unique velocity appearing in the integrating factor of the second postula ...
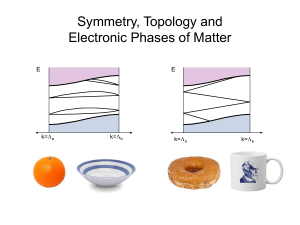
Symmetry, Topology and Electronic Phases of Matter
... 3D Dirac points with strong spin-orbit protected by time reversal symmetry space group symmetries Observed in many real materials ...
... 3D Dirac points with strong spin-orbit protected by time reversal symmetry space group symmetries Observed in many real materials ...
JRC, 14-15 December 2009
... probably not suitable for 100 nm measurements. • Can serve as an internal standard even if used only at 30 and 50 nm. ...
... probably not suitable for 100 nm measurements. • Can serve as an internal standard even if used only at 30 and 50 nm. ...