Centripetal Acceleration
... is proportional to speed squared, implying, for example, that it is four times as ...
... is proportional to speed squared, implying, for example, that it is four times as ...
4.3 Centripetal Acceleration
... is proportional to speed squared, implying, for example, that it is four times as ...
... is proportional to speed squared, implying, for example, that it is four times as ...
Acceleration Analysi..
... felt on our feet or buttocks, is defined by our mass times the acceleration due to gravity or mg. Thus an imposed acceleration of 1 g above the baseline of our gravity, or 2 g's, will be felt as a doubling of our weight. At 6 g's we would feel six times as heavy as normal and would have great diffic ...
... felt on our feet or buttocks, is defined by our mass times the acceleration due to gravity or mg. Thus an imposed acceleration of 1 g above the baseline of our gravity, or 2 g's, will be felt as a doubling of our weight. At 6 g's we would feel six times as heavy as normal and would have great diffic ...
Section 4.3 - CPO Science
... A soccer ball is an example of a projectile. A projectile is an object moving under the influence of only gravity. The path of the ball makes ...
... A soccer ball is an example of a projectile. A projectile is an object moving under the influence of only gravity. The path of the ball makes ...
acceleration
... 5) What is happening at point A in this speed-time graph? A. the object is speeding up B. the object is slowing down C. the object is at ...
... 5) What is happening at point A in this speed-time graph? A. the object is speeding up B. the object is slowing down C. the object is at ...
V - USU Physics
... • Velocity is a vector and represents a bodies speed and direction. • A force must act on a body to change its velocity (i.e. its speed, direction or both). • The force causes the body to accelerate resulting in a change in its velocity. • Acceleration is a vector and represents the rate of change o ...
... • Velocity is a vector and represents a bodies speed and direction. • A force must act on a body to change its velocity (i.e. its speed, direction or both). • The force causes the body to accelerate resulting in a change in its velocity. • Acceleration is a vector and represents the rate of change o ...
Acceleration
... toward a destination is positive displacement; travel back toward the starting position is negative displacement. – The displacement at the end of a walk can be zero for this reason. ...
... toward a destination is positive displacement; travel back toward the starting position is negative displacement. – The displacement at the end of a walk can be zero for this reason. ...
Acceleration
... osculating circle at time t. These components are called thetangential acceleration at and the radial acceleration, respectively. The negative of the radial acceleration is thecentripetal acceleration ac, which points inward, toward the center of curvature.(See Figure 2.) Extension of this approach ...
... osculating circle at time t. These components are called thetangential acceleration at and the radial acceleration, respectively. The negative of the radial acceleration is thecentripetal acceleration ac, which points inward, toward the center of curvature.(See Figure 2.) Extension of this approach ...
Apparently Deriving Fictitious Forces
... should not interfere with ω, as it does if he has mass, due to the need to conserve angular momentum. On the other hand, if we consider him as being a ghost, such a being would feel no force at all acting on it, since its mass is null. So, we decide to let the mass of the observer enter i ...
... should not interfere with ω, as it does if he has mass, due to the need to conserve angular momentum. On the other hand, if we consider him as being a ghost, such a being would feel no force at all acting on it, since its mass is null. So, we decide to let the mass of the observer enter i ...
Acceleration - pruettscience
... Rob is really bored one Saturday night and goes outside to study the nocturnal habits of mice in the hayfield. He sees a mouse sniffing along at 0.1 m/s. but it hears Rob and starts to scurry for safety. In just 3.7 s it accelerates to 0.9 m/s. Find its acceleration. ...
... Rob is really bored one Saturday night and goes outside to study the nocturnal habits of mice in the hayfield. He sees a mouse sniffing along at 0.1 m/s. but it hears Rob and starts to scurry for safety. In just 3.7 s it accelerates to 0.9 m/s. Find its acceleration. ...
Homeroom
... Ama starts sliding with a velocity of 1 m/s. After 3s, her velocity is 7 m/s. What is Ama’s acceleration? What do you know? Initial velocity=1m/s, final velocity=7m/s, time=3s Write the formula: a= v(final)-(V)initial ...
... Ama starts sliding with a velocity of 1 m/s. After 3s, her velocity is 7 m/s. What is Ama’s acceleration? What do you know? Initial velocity=1m/s, final velocity=7m/s, time=3s Write the formula: a= v(final)-(V)initial ...
Lesson 8
... Consider the motion of ball on a circle from point A to point B as shown below. We could describe the path of the ball in Cartesian coordinates or by polar coordinates. In Cartesian coordinate system, we see that both coordinates change!! This makes the problem 2dimensional. ...
... Consider the motion of ball on a circle from point A to point B as shown below. We could describe the path of the ball in Cartesian coordinates or by polar coordinates. In Cartesian coordinate system, we see that both coordinates change!! This makes the problem 2dimensional. ...
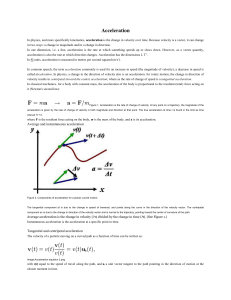
Average Acceleration Instantaneous Acceleration
... 2. Choose a set of coordinate axes and decide which directions are to be called positive and negative. It is often convenient to place the origin at the place where an object starts its motion. In problems involving one dimension, the positive axis is usually chosen to go from left to right. For mot ...
... 2. Choose a set of coordinate axes and decide which directions are to be called positive and negative. It is often convenient to place the origin at the place where an object starts its motion. In problems involving one dimension, the positive axis is usually chosen to go from left to right. For mot ...
2.1 Inertial Frames of Reference
... possibly a temporal coordinate. A frame of reference in which the Law of Inertia holds is an inertial frame or inertial system. An observer at rest (i.e. with zero velocity) in such a system is an inertial observer. Note. The main idea of an inertial observer in an inertial frame is that the observe ...
... possibly a temporal coordinate. A frame of reference in which the Law of Inertia holds is an inertial frame or inertial system. An observer at rest (i.e. with zero velocity) in such a system is an inertial observer. Note. The main idea of an inertial observer in an inertial frame is that the observe ...
Rindler coordinates
In relativistic physics, the Rindler coordinate chart is an important and useful coordinate chart representing part of flat spacetime, also called the Minkowski vacuum. The Rindler coordinate system or frame describes a uniformly accelerating frame of reference in Minkowski space. In special relativity, a uniformly accelerating particle undergoes hyperbolic motion. For each such particle a Rindler frame can be chosen in which it is at rest.The Rindler chart is named after Wolfgang Rindler who popularised its use, although it was already ""well known"" in 1935, according to a paper by Albert Einstein and Nathan Rosen.