Vectors
... If the vector space is orthogonal, each unit vector spanning the space is orthogonal to the other. The collection of the unit vectors that span completely any vector in the vector space is called a basis. In the above, the set of unit vectors { i j } form an orthonormal basis. e.g. A three-dimension ...
... If the vector space is orthogonal, each unit vector spanning the space is orthogonal to the other. The collection of the unit vectors that span completely any vector in the vector space is called a basis. In the above, the set of unit vectors { i j } form an orthonormal basis. e.g. A three-dimension ...
EGR2013 Tutorial 8 Linear Algebra Outline Powers of a Matrix and
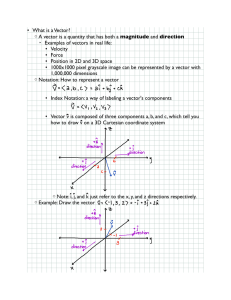
... Definition of Vectors We often use two kinds of quantities, namely scalars and vectors. A scalar is a quantity that is determined by its magnitude; A vector is a quantity that is determined by both its magnitude and its direction. Equality of Vectors: two vectors a and b are equal, if they have the ...
... Definition of Vectors We often use two kinds of quantities, namely scalars and vectors. A scalar is a quantity that is determined by its magnitude; A vector is a quantity that is determined by both its magnitude and its direction. Equality of Vectors: two vectors a and b are equal, if they have the ...
Math 304–504 Linear Algebra Lecture 24: Orthogonal subspaces.
... and nullity of A. Therefore dim V + dim V ⊥ equals the number of columns of A, which is n. ...
... and nullity of A. Therefore dim V + dim V ⊥ equals the number of columns of A, which is n. ...
Lines and planes
... Exercise 8. Find the intersection of the following lines and interpret your result geometrically. −2x + 8y = 3, 3x − 12y = 2. Exercise 9. Find the intersection of the following planes and interpret your result geometrically. 2x + 1y + 3z = 7, 3y + 2z = 8, x + 5y + 6z = 17. Exercise 10. Find the inte ...
... Exercise 8. Find the intersection of the following lines and interpret your result geometrically. −2x + 8y = 3, 3x − 12y = 2. Exercise 9. Find the intersection of the following planes and interpret your result geometrically. 2x + 1y + 3z = 7, 3y + 2z = 8, x + 5y + 6z = 17. Exercise 10. Find the inte ...
Synopsis of Geometric Algebra
... deepest) approach presumes familiarity with the conventional concept of a vector space. Geometric algebras can then be defined simply by specifying appropriate rules for multiplying vectors. That is the approach to be taken here. The terms “linear space” and “vector space” are usually regarded as syn ...
... deepest) approach presumes familiarity with the conventional concept of a vector space. Geometric algebras can then be defined simply by specifying appropriate rules for multiplying vectors. That is the approach to be taken here. The terms “linear space” and “vector space” are usually regarded as syn ...
Linear algebra
... Addition: Place the two vectors tail-to-head and draw the resultant vector. The addition of vectors is commutative (parallelogram law). Rovnoběžník The parallelopiped is the analogue in space of the parallelogram in the plane. ...
... Addition: Place the two vectors tail-to-head and draw the resultant vector. The addition of vectors is commutative (parallelogram law). Rovnoběžník The parallelopiped is the analogue in space of the parallelogram in the plane. ...
Representation of a vector
... Scalar multiplication A vector may also be multiplied by a real number “r”. In mathematics, numbers are often called scalars to distinguish them from vectors, and this operation is therefore called scalar ...
... Scalar multiplication A vector may also be multiplied by a real number “r”. In mathematics, numbers are often called scalars to distinguish them from vectors, and this operation is therefore called scalar ...
Bivector
In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. If a scalar is considered an order zero quantity, and a vector is an order one quantity, then a bivector can be thought of as being of order two. Bivectors have applications in many areas of mathematics and physics. They are related to complex numbers in two dimensions and to both pseudovectors and quaternions in three dimensions. They can be used to generate rotations in any dimension, and are a useful tool for classifying such rotations. They also are used in physics, tying together a number of otherwise unrelated quantities.Bivectors are generated by the exterior product on vectors: given two vectors a and b, their exterior product a ∧ b is a bivector, as is the sum of any bivectors. Not all bivectors can be generated as a single exterior product. More precisely, a bivector that can be expressed as an exterior product is called simple; in up to three dimensions all bivectors are simple, but in higher dimensions this is not the case. The exterior product is antisymmetric, so b ∧ a is the negation of the bivector a ∧ b, producing the opposite orientation, and a ∧ a is the zero bivector.Geometrically, a simple bivector can be interpreted as an oriented plane segment, much as vectors can be thought of as directed line segments. The bivector a ∧ b has a magnitude equal to the area of the parallelogram with edges a and b, has the attitude of the plane spanned by a and b, and has orientation being the sense of the rotation that would align a with b.