Algebraic Topology Lecture Notes Jarah Evslin and
... Global information is important. For example, global data can tell you that it is impossible to define a spinor on a certain space, and so a given spacetime cannot be inhabited by fermions. In general there are both local and global obstructions, with the local obstructions determined by differentia ...
... Global information is important. For example, global data can tell you that it is impossible to define a spinor on a certain space, and so a given spacetime cannot be inhabited by fermions. In general there are both local and global obstructions, with the local obstructions determined by differentia ...
8. Group algebras and Hecke algebras
... and a conformal action of a group G on X such that the following hold. • G = {g ∈ Aut(X) : r ◦ g = r}, so that r : X → T is essentially the quotient map X → X/G. • Let H = {g ∈ G : p ◦ g = p} then the map p : X → S is the quotient map X → X/H. Now let us show how the projection deÞnes a Hecke algebr ...
... and a conformal action of a group G on X such that the following hold. • G = {g ∈ Aut(X) : r ◦ g = r}, so that r : X → T is essentially the quotient map X → X/G. • Let H = {g ∈ G : p ◦ g = p} then the map p : X → S is the quotient map X → X/H. Now let us show how the projection deÞnes a Hecke algebr ...
Stable Models and Circumscription
... according to Remark 1. Consequently, in the t-stable models of (7), t is the transitive closure of p. Similarly, if F is the conjunction of (7) and (8) then SMpt [F ] is equivalent to CIRCpt [F ] and consequently to (9). It is clear from the definition of circumscription that if sentences F and G ar ...
... according to Remark 1. Consequently, in the t-stable models of (7), t is the transitive closure of p. Similarly, if F is the conjunction of (7) and (8) then SMpt [F ] is equivalent to CIRCpt [F ] and consequently to (9). It is clear from the definition of circumscription that if sentences F and G ar ...
Boundaries of CAT(0) Groups and Spaces
... there exists K > 0 such that d(γ(t), γ 0 (t)) ≤ K for any t ∈ [0, +∞). In this case we write γ ∼ γ 0 and we define ∂X := {γ geodesic ray in X}/ ∼ . We call ∂X the boundary of X. In the following we will explore the different topologies that we can use on ∂X. As this definition of the boundary is a d ...
... there exists K > 0 such that d(γ(t), γ 0 (t)) ≤ K for any t ∈ [0, +∞). In this case we write γ ∼ γ 0 and we define ∂X := {γ geodesic ray in X}/ ∼ . We call ∂X the boundary of X. In the following we will explore the different topologies that we can use on ∂X. As this definition of the boundary is a d ...
Homework assignments
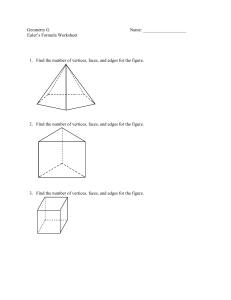
... precisely the interior of some polygon). (a) Prove that χ(X) = V − E + F . (b) The space X is called a regular polytope if all the Pi have the same number r of edges, if each edge in X lies in exactly two faces, and if each vertex in X lies in some fixed number s of faces. Prove that there are preci ...
... precisely the interior of some polygon). (a) Prove that χ(X) = V − E + F . (b) The space X is called a regular polytope if all the Pi have the same number r of edges, if each edge in X lies in exactly two faces, and if each vertex in X lies in some fixed number s of faces. Prove that there are preci ...
Problem Set #1 - University of Chicago Math
... III. Which, if any, among the relations “is finer than”, “is coarser than”, and “is comparable to” forms an equivalence relations among the class of topologies? For those which do not form an equivalence relation, which of the three axioms of an equivalence relation do they satisfy? IV. Complete the ...
... III. Which, if any, among the relations “is finer than”, “is coarser than”, and “is comparable to” forms an equivalence relations among the class of topologies? For those which do not form an equivalence relation, which of the three axioms of an equivalence relation do they satisfy? IV. Complete the ...
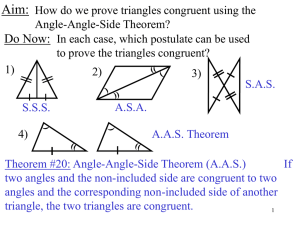
AAS Theorem - Math Story
... Do Now: In each case, which postulate can be used to prove the triangles congruent? ...
... Do Now: In each case, which postulate can be used to prove the triangles congruent? ...
foundations of algebraic geometry class 38
... functor”, and corresponds to the fact that we get a long exact sequence in cohomology extending to the right (from the 0th terms). Later this year, we will see that in good circumstances, if we have a left-exact functor, there is be a long exact sequence going off to the right, in terms of right der ...
... functor”, and corresponds to the fact that we get a long exact sequence in cohomology extending to the right (from the 0th terms). Later this year, we will see that in good circumstances, if we have a left-exact functor, there is be a long exact sequence going off to the right, in terms of right der ...
Group action
In mathematics, a symmetry group is an abstraction used to describe the symmetries of an object. A group action formalizes of the relationship between the group and the symmetries of the object. It relates each element of the group to a particular transformation of the object.In this case, the group is also called a permutation group (especially if the set is finite or not a vector space) or transformation group (especially if the set is a vector space and the group acts like linear transformations of the set). A permutation representation of a group G is a representation of G as a group of permutations of the set (usually if the set is finite), and may be described as a group representation of G by permutation matrices. It is the same as a group action of G on an ordered basis of a vector space.A group action is an extension to the notion of a symmetry group in which every element of the group ""acts"" like a bijective transformation (or ""symmetry"") of some set, without being identified with that transformation. This allows for a more comprehensive description of the symmetries of an object, such as a polyhedron, by allowing the same group to act on several different sets of features, such as the set of vertices, the set of edges and the set of faces of the polyhedron.If G is a group and X is a set, then a group action may be defined as a group homomorphism h from G to the symmetric group on X. The action assigns a permutation of X to each element of the group in such a way that the permutation of X assigned to the identity element of G is the identity transformation of X; a product gk of two elements of G is the composition of the permutations assigned to g and k.The abstraction provided by group actions is a powerful one, because it allows geometrical ideas to be applied to more abstract objects. Many objects in mathematics have natural group actions defined on them. In particular, groups can act on other groups, or even on themselves. Despite this generality, the theory of group actions contains wide-reaching theorems, such as the orbit stabilizer theorem, which can be used to prove deep results in several fields.