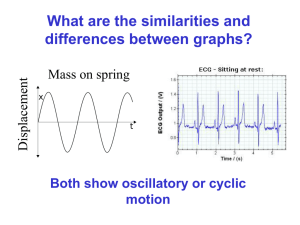
shm INTRO - Mrs Physics
... oscillations of SHM retain the same magnitude indefinitely. In real systems energy is lost from the system due to factors such as air resistance and friction in bearings and pivots, thus the amplitude of the SHM steadily decreases. This removal of energy is called damping. SHM in a system such as a ...
... oscillations of SHM retain the same magnitude indefinitely. In real systems energy is lost from the system due to factors such as air resistance and friction in bearings and pivots, thus the amplitude of the SHM steadily decreases. This removal of energy is called damping. SHM in a system such as a ...
Unit 2 Exam Study Guide
... downward upon your body. The reaction force to the force of the Earth pulling you downward is ___. a. the force of the chair pushing you upward b. the force of the floor pushing your chair upward c. the force of the Earth pushing you upward d. the force of your body pulling the Earth upwards 13. A g ...
... downward upon your body. The reaction force to the force of the Earth pulling you downward is ___. a. the force of the chair pushing you upward b. the force of the floor pushing your chair upward c. the force of the Earth pushing you upward d. the force of your body pulling the Earth upwards 13. A g ...
Document
... The previous image shows a system that is underdamped – it goes through multiple oscillations before coming to rest. A critically damped system is one that relaxes back to the equilibrium position without oscillating and in minimum time; an overdamped system will also not oscillate but is damped so ...
... The previous image shows a system that is underdamped – it goes through multiple oscillations before coming to rest. A critically damped system is one that relaxes back to the equilibrium position without oscillating and in minimum time; an overdamped system will also not oscillate but is damped so ...
香港考試局
... the mass is pulled down 4 cm from its equilibrium position and released from rest, it takes 0.6 s to rise back to its equilibrium position. If the mass is pulled down 5 cm from its equilibrium position and released from rest, how long does it take for the mass to rise 4 cm ? (Assume that the spring ...
... the mass is pulled down 4 cm from its equilibrium position and released from rest, it takes 0.6 s to rise back to its equilibrium position. If the mass is pulled down 5 cm from its equilibrium position and released from rest, how long does it take for the mass to rise 4 cm ? (Assume that the spring ...
11-2 Vector Cross Product
... 11-1 Angular Momentum—Objects Rotating About a Fixed Axis The rotational analog of linear momentum is angular momentum, L: Then the rotational analog of Newton’s second law is: This form of Newton’s second law is valid even if I is not constant. ...
... 11-1 Angular Momentum—Objects Rotating About a Fixed Axis The rotational analog of linear momentum is angular momentum, L: Then the rotational analog of Newton’s second law is: This form of Newton’s second law is valid even if I is not constant. ...
Oaks_Park - TuHS Physics Homepage
... B) Energy Estimate the mass of the locomotive, the train and its riders. (in kg) (Pick a representative car, count the people and multiply by 70 kg or so, and guess for the car. add 'em all up) Use your calculated velocity from A) to calculate the maximum kinetic energy of the train. (5 pts) C) Dyna ...
... B) Energy Estimate the mass of the locomotive, the train and its riders. (in kg) (Pick a representative car, count the people and multiply by 70 kg or so, and guess for the car. add 'em all up) Use your calculated velocity from A) to calculate the maximum kinetic energy of the train. (5 pts) C) Dyna ...
Producing RHS of Acceleration Eq.
... Take one time derivative of constraints (q,t) to obtain the velocity equation: ...
... Take one time derivative of constraints (q,t) to obtain the velocity equation: ...
Class Notes - St. Bonaventure University
... Now, the amount of a physical quantity remains the same, no matter what system of units is used to obtain a numerical measure of that quantity. For instance, we might measure the length of an (American) football field with a meter stick and a yard stick. We’d get two different numerical values, but ...
... Now, the amount of a physical quantity remains the same, no matter what system of units is used to obtain a numerical measure of that quantity. For instance, we might measure the length of an (American) football field with a meter stick and a yard stick. We’d get two different numerical values, but ...
rate of change
... This is not the same acceleration you would measure at a fixed point in the fluid, the Eulerian acceleration. With Lagrangian dynamics, we ...
... This is not the same acceleration you would measure at a fixed point in the fluid, the Eulerian acceleration. With Lagrangian dynamics, we ...
Teaching six simple machines to middle school students
... would be 1/10. • Since there are 10 threads per inch of screw, the distance between two adjacent screw threads is 1/10 of an inch. Also, remember that one complete revolution of a screw will move the screw into an object a distance equal to the pitch of the screw. Therefore, one complete revolution ...
... would be 1/10. • Since there are 10 threads per inch of screw, the distance between two adjacent screw threads is 1/10 of an inch. Also, remember that one complete revolution of a screw will move the screw into an object a distance equal to the pitch of the screw. Therefore, one complete revolution ...
Uniform Circular Motion
... • Circular path • Must be an unbalanced force acting towards axis of rotation- think free body diagrams! • Ex of forces: tension, banked curves, gravitation ...
... • Circular path • Must be an unbalanced force acting towards axis of rotation- think free body diagrams! • Ex of forces: tension, banked curves, gravitation ...
NEWTON`S LESSON 9
... Note that the vertical forces balance but the horizontal forces do not. The net force is Fnet = 129.9 N, right - 60 N, left = 69.9 N, right The mass is m = (Fgrav / g) = 20 kg So the acceleration is a = (69.9 N) / (20 kg) =3.50 m/s/s. ...
... Note that the vertical forces balance but the horizontal forces do not. The net force is Fnet = 129.9 N, right - 60 N, left = 69.9 N, right The mass is m = (Fgrav / g) = 20 kg So the acceleration is a = (69.9 N) / (20 kg) =3.50 m/s/s. ...