Matter – Chemical and Physical Properties
... atomic bonding – linking together of atoms to form larger structures, including solids Types of Bonds Covalent bond – one or more electrons are shared between two atoms Ionic bond – one or more electrons are transferred from one atom to another Metallic bond – described as a “sea of electrons”. Elec ...
... atomic bonding – linking together of atoms to form larger structures, including solids Types of Bonds Covalent bond – one or more electrons are shared between two atoms Ionic bond – one or more electrons are transferred from one atom to another Metallic bond – described as a “sea of electrons”. Elec ...
FLUID FLOW IDEAL FLUID BERNOULLI`S PRINCIPLE
... BERNOULLI'S EQUATION (conservation of ENERGY) An interesting effect is that, for a fluid (e.g. air) flowing through a pipe with a constriction in it, the fluid pressure is lowest at the constriction. In terms of the equation of continuity the fluid pressure falls as the flow speed increases. The rea ...
... BERNOULLI'S EQUATION (conservation of ENERGY) An interesting effect is that, for a fluid (e.g. air) flowing through a pipe with a constriction in it, the fluid pressure is lowest at the constriction. In terms of the equation of continuity the fluid pressure falls as the flow speed increases. The rea ...
Unsteady MHD Couette Flow with Heat Transfer of a Viscoelastic
... steady state, the fluid behaves like a viscous fluid without elasticity. Solving Eq. (2) for txy in terms of the velocity component u we obtain ...
... steady state, the fluid behaves like a viscous fluid without elasticity. Solving Eq. (2) for txy in terms of the velocity component u we obtain ...
Lecture 26 - Pascal`s Principle
... h = Patmos / ρg = 105 / (1000 x 9.8) ~ 10 m! That's why the jar+sheet demo works - atmospheric pressure can balance 10 m of H2O. Pascal's Principle Lastly, we consider what happens when an external pressure is applied to a confined fluid. We already know that the pressure varies locally with positio ...
... h = Patmos / ρg = 105 / (1000 x 9.8) ~ 10 m! That's why the jar+sheet demo works - atmospheric pressure can balance 10 m of H2O. Pascal's Principle Lastly, we consider what happens when an external pressure is applied to a confined fluid. We already know that the pressure varies locally with positio ...
Chapter 3 General Molecular transport Equation for Momentum, Heat
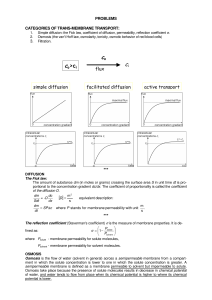
... General molecular transport equation driving force rate of a transfer process resistance d For molecular transport or ...
... General molecular transport equation driving force rate of a transfer process resistance d For molecular transport or ...
Fluids - Northern Illinois University
... In a Lagrangian view the total time derivative depends on position and time. An Eulerian view is just the partial derivative with time. • Points are fixed ...
... In a Lagrangian view the total time derivative depends on position and time. An Eulerian view is just the partial derivative with time. • Points are fixed ...
sensors homework 3
... surroundings. Heat transfer depends on the flow velocity. The flow field information around the surface of an object could be divided into two components, that is, the normal pressure exerted on the surface and the shear stress along the surface. Both of the components are useful for inferring the f ...
... surroundings. Heat transfer depends on the flow velocity. The flow field information around the surface of an object could be divided into two components, that is, the normal pressure exerted on the surface and the shear stress along the surface. Both of the components are useful for inferring the f ...
the fluid mechanics course, CHE 204, Transport Phenomena I
... deformation can “remember” their recent molecular configurations, and in attempting to recover their recent states, they will exhibit elasticity in addition to viscosity. Other fluids, such as drilling mud or toothpaste, behave essentially as solids and will not flow when subject to small shear forc ...
... deformation can “remember” their recent molecular configurations, and in attempting to recover their recent states, they will exhibit elasticity in addition to viscosity. Other fluids, such as drilling mud or toothpaste, behave essentially as solids and will not flow when subject to small shear forc ...
Fluid dynamics
In physics, fluid dynamics is a subdiscipline of fluid mechanics that deals with fluid flow—the natural science of fluids (liquids and gases) in motion. It has several subdisciplines itself, including aerodynamics (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Some of its principles are even used in traffic engineering, where traffic is treated as a continuous fluid, and crowd dynamics. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves calculating various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space and time.Before the twentieth century, hydrodynamics was synonymous with fluid dynamics. This is still reflected in names of some fluid dynamics topics, like magnetohydrodynamics and hydrodynamic stability, both of which can also be applied to gases.