Ph211_CH5_worksheet-f06
... Since the masses are attached their accelerations are equal: a1y = a2x = asystem Solving for asystem: m2gsin – m1asystem - m1g = m2asystem asystem = (m2gsin – m1g)/(m1 + m2) = -1.03 m/s2 (i.e. up the incline!) e. What are the tension forces acting on each mass? Express the tension vectors in compo ...
... Since the masses are attached their accelerations are equal: a1y = a2x = asystem Solving for asystem: m2gsin – m1asystem - m1g = m2asystem asystem = (m2gsin – m1g)/(m1 + m2) = -1.03 m/s2 (i.e. up the incline!) e. What are the tension forces acting on each mass? Express the tension vectors in compo ...
0BJECTIVES 7
... ____ 13. The average acceleration of a car that goes from 0 m/s to 25 m/s in 8.0s is a. 0.32 m/s c. 3.1 m/s b. 0.32 m/s2 d. 3.1 m/s2 ____ 14. Which of the following does not indicate velocity? a. 14 m/s SSE b. 40 km/h toward the town square along the main street c. 80 km/h going from New York toward ...
... ____ 13. The average acceleration of a car that goes from 0 m/s to 25 m/s in 8.0s is a. 0.32 m/s c. 3.1 m/s b. 0.32 m/s2 d. 3.1 m/s2 ____ 14. Which of the following does not indicate velocity? a. 14 m/s SSE b. 40 km/h toward the town square along the main street c. 80 km/h going from New York toward ...
Chap04-2014
... ideal case of zero resistance, horizontal motion would never stop. Galileo was the first to recognize that the general principles of motion could be found by extrapolating experimental results to the ideal case, in which there is no resistance to slow down an object’s motion. ...
... ideal case of zero resistance, horizontal motion would never stop. Galileo was the first to recognize that the general principles of motion could be found by extrapolating experimental results to the ideal case, in which there is no resistance to slow down an object’s motion. ...
Plan for March 2010
... In an interaction between body A and body B, body A exerts a force on body B and body B exerts an equal and opposite force on body A. These equal and opposite forces of an interaction never act on the same body, because an interaction is between bodies. This insight is not only a description of inte ...
... In an interaction between body A and body B, body A exerts a force on body B and body B exerts an equal and opposite force on body A. These equal and opposite forces of an interaction never act on the same body, because an interaction is between bodies. This insight is not only a description of inte ...
class slides for Chapter 4
... •“Objects at rest tend to stay at rest and objects in motion tend to stay in motion.” •What that common statement of the first law often leaves out is the final phrase “until acted upon an external force”. ...
... •“Objects at rest tend to stay at rest and objects in motion tend to stay in motion.” •What that common statement of the first law often leaves out is the final phrase “until acted upon an external force”. ...
File
... • The force exerted by the surrounding air increases with the increasing falling speed. • The force of air resistance may continue to increase until it equals the weight. At this point, the net force is zero and no further acceleration occurs. The object has reached terminal velocity and continues t ...
... • The force exerted by the surrounding air increases with the increasing falling speed. • The force of air resistance may continue to increase until it equals the weight. At this point, the net force is zero and no further acceleration occurs. The object has reached terminal velocity and continues t ...
Presentation
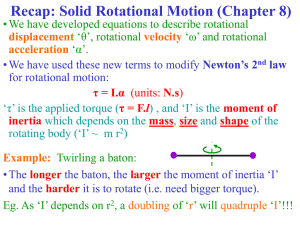
... mass m and radius r. The three objects are arranged so that an axis of rotation passes through the center of each object. The rotation axis is perpendicular to the plane of the flat disk. Which of the three objects has the largest moment of inertia? a) The solid sphere and hollow sphere have the sam ...
... mass m and radius r. The three objects are arranged so that an axis of rotation passes through the center of each object. The rotation axis is perpendicular to the plane of the flat disk. Which of the three objects has the largest moment of inertia? a) The solid sphere and hollow sphere have the sam ...
6 Newton`s Second Law of Motion–Force and
... Both liquids and gases are called fluids because they flow. • Fluid friction occurs as an object pushes aside the fluid it is moving through. • The friction of liquids is appreciable, even at low speeds. • Air resistance is the friction acting on something moving through air. ...
... Both liquids and gases are called fluids because they flow. • Fluid friction occurs as an object pushes aside the fluid it is moving through. • The friction of liquids is appreciable, even at low speeds. • Air resistance is the friction acting on something moving through air. ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.