Newton Review
... Speed = Distance/ Time; 20 ft/s = 200 ft/10 s 13. What is the acceleration of an object that goes from 50 m/s to 100 m/s in 10 seconds? ∆ speed/time = acceleration; 100 m/s – 50 m/s / 10 s = 50 m/s / 10 s = 5 m/s2 Fill in the blanks for the following questions below. 14. Air resistance is a kind of ...
... Speed = Distance/ Time; 20 ft/s = 200 ft/10 s 13. What is the acceleration of an object that goes from 50 m/s to 100 m/s in 10 seconds? ∆ speed/time = acceleration; 100 m/s – 50 m/s / 10 s = 50 m/s / 10 s = 5 m/s2 Fill in the blanks for the following questions below. 14. Air resistance is a kind of ...
Homework 8
... Find the hamiltonian, H for a mass m confined to the x axis and subject to a force F = −kx3 where k > 0. Sketch and describe the phase-space orbits. A beam of protons is moving along an accelerator pipe in the z-direction. The particles are uniformly distributed in a cylindrical volume of length L0 ...
... Find the hamiltonian, H for a mass m confined to the x axis and subject to a force F = −kx3 where k > 0. Sketch and describe the phase-space orbits. A beam of protons is moving along an accelerator pipe in the z-direction. The particles are uniformly distributed in a cylindrical volume of length L0 ...
Kinematics, Momentum and Energy
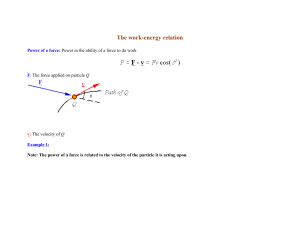
... When a force is applied to an object, it will be accelerated. ...
... When a force is applied to an object, it will be accelerated. ...
revised newton pres
... • Law I: Every body persists in the state of rest or moving uniformly straight, except when it is compelled to change its state by the force impressed upon it. This is called Inertia. • Galileo actually discovered inertia, but Newton rephrased it. DUDE YOU THIEF! ...
... • Law I: Every body persists in the state of rest or moving uniformly straight, except when it is compelled to change its state by the force impressed upon it. This is called Inertia. • Galileo actually discovered inertia, but Newton rephrased it. DUDE YOU THIEF! ...
Magic Square Vocabulary Game Combinations
... D. Speed E. Acceleration F. Velocity G. Friction H. 3rd Law of Motion I. Gravitational Force ...
... D. Speed E. Acceleration F. Velocity G. Friction H. 3rd Law of Motion I. Gravitational Force ...
Life Science - Tom R. Chambers
... The first law deals with forces and changes in velocity. For just a moment, let us imagine that you can apply only one force to an object. That is, you could choose push the object to the right or you could choose to push it to the left, but not to the left and right at the same time, and also not u ...
... The first law deals with forces and changes in velocity. For just a moment, let us imagine that you can apply only one force to an object. That is, you could choose push the object to the right or you could choose to push it to the left, but not to the left and right at the same time, and also not u ...
Motion In Review
... • It gives everything a weight • If gravity didn’t exist we would float around like astronauts in space ...
... • It gives everything a weight • If gravity didn’t exist we would float around like astronauts in space ...
1 Newton`s Law of Universal Gravitation (Ch 13) Law of Gravitation
... Using the distance between the Earth and the Sun, and the period of the Earth’s orbit, Kepler’s Third Law can be used to find the mass of the Sun ...
... Using the distance between the Earth and the Sun, and the period of the Earth’s orbit, Kepler’s Third Law can be used to find the mass of the Sun ...
Sects. 6.5 through 6.9
... A particle is attached between two identical springs on a horizontal frictionless table. Both springs have spring constant k and are initially unstressed. (a) The particle is pulled a distance x along a direction perpendicular to the initial configuration of the springs. Show that the force exerted ...
... A particle is attached between two identical springs on a horizontal frictionless table. Both springs have spring constant k and are initially unstressed. (a) The particle is pulled a distance x along a direction perpendicular to the initial configuration of the springs. Show that the force exerted ...
M - Otterbein University
... • Apparent brightness of objects that reflect sunlight do depends on three things: – Size of the object (the bigger the brighter) – Distance to the object (the closer the brighter) – “Surface” properties of the object (the whiter the brighter, the darker the dimmer) • Technical term: Albedo (Albedo ...
... • Apparent brightness of objects that reflect sunlight do depends on three things: – Size of the object (the bigger the brighter) – Distance to the object (the closer the brighter) – “Surface” properties of the object (the whiter the brighter, the darker the dimmer) • Technical term: Albedo (Albedo ...
Newton`s Second Law
... motionless until a force is applied (a kick). The kicked ball rolls until the force of friction between the ball and the grass acts on the ball and slows it. ...
... motionless until a force is applied (a kick). The kicked ball rolls until the force of friction between the ball and the grass acts on the ball and slows it. ...
Topics covered in PH111 - Rose
... the equations of motion at constant acceleration from velocity-time graph, projectile motion: constant acceleration equations for vertical and horizontal motions, definition of period, angular velocity and acceleration, relation between linear and angular terms, centripetal and tangential accelerati ...
... the equations of motion at constant acceleration from velocity-time graph, projectile motion: constant acceleration equations for vertical and horizontal motions, definition of period, angular velocity and acceleration, relation between linear and angular terms, centripetal and tangential accelerati ...
PHYS4330 Theoretical Mechanics HW #1 Due 6 Sept 2011
... (1) A particle of mass m moves in one dimension x. It is subject to a force F (t) = F0 e−t/τ , where τ is a positive constant, and starts from rest at x = 0 and t = 0. Find the velocity v(t) = ẋ(t) and position x(t) as functions of time. Also find the velocity v(t) for times t � τ . (2) A particle ...
... (1) A particle of mass m moves in one dimension x. It is subject to a force F (t) = F0 e−t/τ , where τ is a positive constant, and starts from rest at x = 0 and t = 0. Find the velocity v(t) = ẋ(t) and position x(t) as functions of time. Also find the velocity v(t) for times t � τ . (2) A particle ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.