Quantum Mechanics II, Ex 4730
... Given a spherical shell with radius R and a particle with mass M and charge e. Notice that the standard variables which show the particle are (θ, φ, Lx, Ly, Lz) In this question we have to assume that the particle can be excited from ground state to first energy level but not beyond so the state spa ...
... Given a spherical shell with radius R and a particle with mass M and charge e. Notice that the standard variables which show the particle are (θ, φ, Lx, Ly, Lz) In this question we have to assume that the particle can be excited from ground state to first energy level but not beyond so the state spa ...
Cut squares along dotted line then fold in half to make flashcard
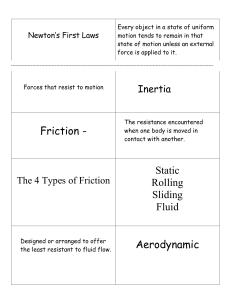
... Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it. ...
... Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it. ...
Nuclear Forces
... • Newton's second law of motion can be formally stated as follows: • The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object. In terms of an equat ...
... • Newton's second law of motion can be formally stated as follows: • The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object. In terms of an equat ...
Examples of Newton`s 1 st Law
... and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force. ...
... and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an unbalanced force. ...
Study Guide For Unit 6 Test
... 10. When an 20 Newton potato gun is fired, a .05 kg potato receives an acceleration of 100 m/s2 while it is in the tube. a. How much force acts on the potato? ...
... 10. When an 20 Newton potato gun is fired, a .05 kg potato receives an acceleration of 100 m/s2 while it is in the tube. a. How much force acts on the potato? ...
Review Sheet with Answers
... 16. Are the forces balanced or unbalanced? A. A person sitting on a chair balanced B. 20 N left and 30 N right unbalanced C. An object at constant speed balanced D. An accelerating plane unbalanced E. A stopping car unbalanced ...
... 16. Are the forces balanced or unbalanced? A. A person sitting on a chair balanced B. 20 N left and 30 N right unbalanced C. An object at constant speed balanced D. An accelerating plane unbalanced E. A stopping car unbalanced ...
Chapter Summary
... the object either remains at rest or it keeps moving with constant velocity. If there is a non-zero net force acting, then the object's velocity changes. Newton’s Second Law tells us that the connection between an object’s net force and its acceleration is given by: , which we can re-write as ...
... the object either remains at rest or it keeps moving with constant velocity. If there is a non-zero net force acting, then the object's velocity changes. Newton’s Second Law tells us that the connection between an object’s net force and its acceleration is given by: , which we can re-write as ...
NAME________ DATE
... (____________). Force (n)= Mass (kg) times Acceleration (m/s2) Force = mass * change in speed / time The force needed to change speed is proportional to the ____, also, the larger the mass, the ____ the _____________. (note: the first law is a special case of the second law, f=ma with the force and ...
... (____________). Force (n)= Mass (kg) times Acceleration (m/s2) Force = mass * change in speed / time The force needed to change speed is proportional to the ____, also, the larger the mass, the ____ the _____________. (note: the first law is a special case of the second law, f=ma with the force and ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.