Electricity - Learning on the Loop
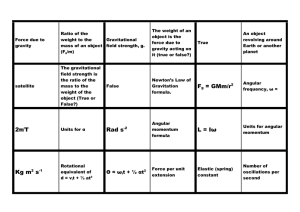
... field strength is the ratio of the mass to the weight of the object (True or False?) ...
... field strength is the ratio of the mass to the weight of the object (True or False?) ...
Introduction to Circular Motion
... The direction of the velocity is tangent to the circle at all points. If the string was to break, the mass the mass would move in a straight line tangent to the circle. If gravity is negligible then the net force would be zero and Newton's first law would apply. (c) What is the direction of the acce ...
... The direction of the velocity is tangent to the circle at all points. If the string was to break, the mass the mass would move in a straight line tangent to the circle. If gravity is negligible then the net force would be zero and Newton's first law would apply. (c) What is the direction of the acce ...
Review for Intro. Physics Part A Final Exam
... bicycle goes from rest to 5km/h which has a a) car greater b) bike acceleration? c) same same d) I don’t know ...
... bicycle goes from rest to 5km/h which has a a) car greater b) bike acceleration? c) same same d) I don’t know ...
Newtons 1st Law notes
... Balanced Forces Net Force—when 2 or more forces act on an object at the same time The object does not move if the forces cancel each other out. Balanced Forces—forces on an object that are equal in size and opposite in direction. ...
... Balanced Forces Net Force—when 2 or more forces act on an object at the same time The object does not move if the forces cancel each other out. Balanced Forces—forces on an object that are equal in size and opposite in direction. ...
Part I
... Newton’s First Law • 1st Law: (“Law of Inertia”): “In the absence of external forces and when viewed from an inertial reference frame, an object at rest remains at rest and an object in motion remains in motion with a constant velocity (constant speed in a straight line).” Sir Isaac Newton as an ...
... Newton’s First Law • 1st Law: (“Law of Inertia”): “In the absence of external forces and when viewed from an inertial reference frame, an object at rest remains at rest and an object in motion remains in motion with a constant velocity (constant speed in a straight line).” Sir Isaac Newton as an ...
Newton`s Second Law
... Acceleration, as = P/ms = (36 N)/(11,000 kg) = 0.0033 m/s2 The spacecraft exerts an equal and opposite force on the astronaut, so the force on the astronaut is –P (Newton’s 3rd law). Acceleration, aa = –P/ma = (–36 N)/(92 kg) = –0.39 m/s2 ...
... Acceleration, as = P/ms = (36 N)/(11,000 kg) = 0.0033 m/s2 The spacecraft exerts an equal and opposite force on the astronaut, so the force on the astronaut is –P (Newton’s 3rd law). Acceleration, aa = –P/ma = (–36 N)/(92 kg) = –0.39 m/s2 ...
Newtons Laws of Motion_ppt_RevW10
... at her with a greater speed it will have a greater inertia. Sally argues that inertia does not depend upon speed, but rather upon mass. With whom do you agree? A)Harry B)Sally ...
... at her with a greater speed it will have a greater inertia. Sally argues that inertia does not depend upon speed, but rather upon mass. With whom do you agree? A)Harry B)Sally ...
NEWTONS LAW`S OF MOTION
... velocity (acceleration )of an object is proportional to the force and in the direction of force. • Similarly it takes less stopping force to stop an object moving with less velocity (acceleration) ...
... velocity (acceleration )of an object is proportional to the force and in the direction of force. • Similarly it takes less stopping force to stop an object moving with less velocity (acceleration) ...
Jeopardy - QuestGarden.com
... equal pull, the reason the Earth goes around the Sun and not the other way round is due to the Sun’s _____ ______ ...
... equal pull, the reason the Earth goes around the Sun and not the other way round is due to the Sun’s _____ ______ ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.