Giancoli Ch 8.Word
... 33. The force to produce the required torque is Fwrench = /L = (80 m · N)/(0.30 m) = 2.7 102 N. Because this torque is balanced by the torque produced by the bolt on the wrench, an equal torque is produced on the bolt. Because there are six points where a force is applied to the bolt, we have Fbo ...
... 33. The force to produce the required torque is Fwrench = /L = (80 m · N)/(0.30 m) = 2.7 102 N. Because this torque is balanced by the torque produced by the bolt on the wrench, an equal torque is produced on the bolt. Because there are six points where a force is applied to the bolt, we have Fbo ...
Section 4 Seesaws Seesaws are a simply toy that consists of a long
... Well, physicists and mathematicians distinguish them using a convention known as the right-hand rule and the right-hand rule says that if you take your fingers of your right hand and curl them in the direction in which the rotation occurs. For example, if I'm going from this to this, the rotation i ...
... Well, physicists and mathematicians distinguish them using a convention known as the right-hand rule and the right-hand rule says that if you take your fingers of your right hand and curl them in the direction in which the rotation occurs. For example, if I'm going from this to this, the rotation i ...
Section 4 Seesaws Seesaws are a simply toy
... and have some fun. I'm going to throw a riderless, unsupported seesaw, well that sure was quick. But this is video so I can show you that throw again and this time I can slow it down to one tenth its original speed. Moreover, I can make the images of the seesaw linger on the screen so that you can ...
... and have some fun. I'm going to throw a riderless, unsupported seesaw, well that sure was quick. But this is video so I can show you that throw again and this time I can slow it down to one tenth its original speed. Moreover, I can make the images of the seesaw linger on the screen so that you can ...
Section 4 Seesaws Hello. I`m Lou Bloomfield and welcome to How
... Pick your unit of angle and stick with it. You're fine. So you can describe this angular position as 90 degrees down. Or quarter rotation down. Or pi over two radians down. They're all the same. That's angular position, but that by itself doesn't help us redraft Newton's first law of rotational moti ...
... Pick your unit of angle and stick with it. You're fine. So you can describe this angular position as 90 degrees down. Or quarter rotation down. Or pi over two radians down. They're all the same. That's angular position, but that by itself doesn't help us redraft Newton's first law of rotational moti ...
RADIATION REACTION AND SELF-FORCE IN CURVED SPACETIME IN A FIELD THEORY APPROACH
... the post-Newtonian (PN) formalism, which assumes that the two bodies, possibly spinning, are weakly gravitating sources moving at slow velocities under their mutual gravitational influences. Recently, the equations of motion for the two bodies and the radiation these emit have been computed using th ...
... the post-Newtonian (PN) formalism, which assumes that the two bodies, possibly spinning, are weakly gravitating sources moving at slow velocities under their mutual gravitational influences. Recently, the equations of motion for the two bodies and the radiation these emit have been computed using th ...
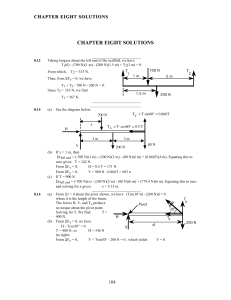
Ch 5 Solutions Glencoe 2013
... 34. Ryan and Becca are moving a folding table out of the sunlight. A cup of lemonade, with a mass of 0.44 kg, is on the table. Becca lifts her end of the table before Ryan does, and as a result, the table makes an angle of 15.0° with the horizontal. Find the components of the cup’s weight that are ...
... 34. Ryan and Becca are moving a folding table out of the sunlight. A cup of lemonade, with a mass of 0.44 kg, is on the table. Becca lifts her end of the table before Ryan does, and as a result, the table makes an angle of 15.0° with the horizontal. Find the components of the cup’s weight that are ...
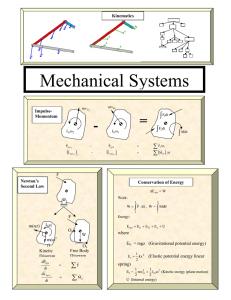
momentum
... If you wish to increase the momentum of something as much as possible, you not only apply the greatest force you can, you also extend the time of application as much as possible. Long-range cannons have long barrels. The longer the barrel, the greater the velocity of the emerging cannonball or shell ...
... If you wish to increase the momentum of something as much as possible, you not only apply the greatest force you can, you also extend the time of application as much as possible. Long-range cannons have long barrels. The longer the barrel, the greater the velocity of the emerging cannonball or shell ...
Ex. 37 PowerPoint
... When an object is accelerated, work is being done. When an object is decelerated, the kinetic energy it has must be dissipated (reduced to zero). When stopping a car, work is done by the brakes (friction) to dissipate the energy. The EK of the car is transformed into heat and sound. The fact that th ...
... When an object is accelerated, work is being done. When an object is decelerated, the kinetic energy it has must be dissipated (reduced to zero). When stopping a car, work is done by the brakes (friction) to dissipate the energy. The EK of the car is transformed into heat and sound. The fact that th ...
(1 Of 2) Air Track TEACHER
... are the final momenta of those objects. In an elastic collision, kinetic energy is also conserved: ½m1v1i2 + ½m2v2i2 = ½m1v1f2 + ½m2v2f2 where the terms on the left side of the equation are the initial kinetic energies of the objects in the collision, and the terms on the right side of the equation ...
... are the final momenta of those objects. In an elastic collision, kinetic energy is also conserved: ½m1v1i2 + ½m2v2i2 = ½m1v1f2 + ½m2v2f2 where the terms on the left side of the equation are the initial kinetic energies of the objects in the collision, and the terms on the right side of the equation ...
1 A 0.40 kg toy car moves at constant acceleration of 2.3 m/s2
... A stationary 2.0 kg object is located on a table near the surface of the earth. The coefficient of static friction between the surfaces is 0.80 and the coefficient of kinetic friction is 0.65. 64 A horizontal force of 10 N is applied to the object. A Draw a free body diagram with the forces to scale ...
... A stationary 2.0 kg object is located on a table near the surface of the earth. The coefficient of static friction between the surfaces is 0.80 and the coefficient of kinetic friction is 0.65. 64 A horizontal force of 10 N is applied to the object. A Draw a free body diagram with the forces to scale ...
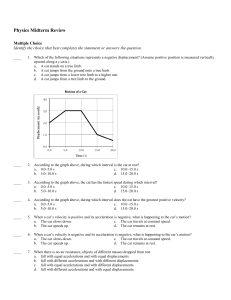
Physics Midterm Review Multiple Choice Identify the choice that best
... 53. Why does it require much less force to accelerate a low-mass object than it does to accelerate a high-mass object the same amount? 54. How do mass and weight vary with altitude? 55. Distinguish between mass and weight. 56. When a car is moving, what happens to the velocity and acceleration of th ...
... 53. Why does it require much less force to accelerate a low-mass object than it does to accelerate a high-mass object the same amount? 54. How do mass and weight vary with altitude? 55. Distinguish between mass and weight. 56. When a car is moving, what happens to the velocity and acceleration of th ...
Newton's theorem of revolving orbits
In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion (Figures 1 and 2). Newton applied his theorem to understanding the overall rotation of orbits (apsidal precession, Figure 3) that is observed for the Moon and planets. The term ""radial motion"" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.Isaac Newton derived this theorem in Propositions 43–45 of Book I of his Philosophiæ Naturalis Principia Mathematica, first published in 1687. In Proposition 43, he showed that the added force must be a central force, one whose magnitude depends only upon the distance r between the particle and a point fixed in space (the center). In Proposition 44, he derived a formula for the force, showing that it was an inverse-cube force, one that varies as the inverse cube of r. In Proposition 45 Newton extended his theorem to arbitrary central forces by assuming that the particle moved in nearly circular orbit.As noted by astrophysicist Subrahmanyan Chandrasekhar in his 1995 commentary on Newton's Principia, this theorem remained largely unknown and undeveloped for over three centuries. Since 1997, the theorem has been studied by Donald Lynden-Bell and collaborators. Its first exact extension came in 2000 with the work of Mahomed and Vawda.