Chapter 13 Slide
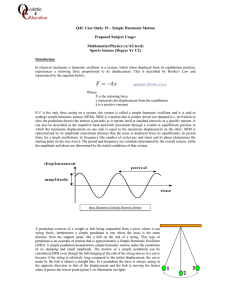
... x is the position at time t x varies between +A and –A ω– angular frequency of oscillations, units: radians per second [rad/s] ω = 2πf; f – frequency of oscillations, units: s-1 or Hertz [Hz] f = 1/T , T period of oscillations ...
... x is the position at time t x varies between +A and –A ω– angular frequency of oscillations, units: radians per second [rad/s] ω = 2πf; f – frequency of oscillations, units: s-1 or Hertz [Hz] f = 1/T , T period of oscillations ...
Stochastic flows associated to coalescent processes II: Stochastic
... In a previous work [1], we obtained a surprising connection between the class of exchangeable coalescents and certain remarkable stochastic flows on the interval [0, 1]. The main purpose of the present paper is to derive more explicit information about these flows, and in particular to represent the ...
... In a previous work [1], we obtained a surprising connection between the class of exchangeable coalescents and certain remarkable stochastic flows on the interval [0, 1]. The main purpose of the present paper is to derive more explicit information about these flows, and in particular to represent the ...
Monday, April 7, 2008 - UTA HEP WWW Home Page
... external forces exerting on it. What is the impact of Newton’s 3rd Law? If particle#1 exerts force on particle #2, there must be another force that the particle #2 exerts on #1 as the reaction force. Both the forces are internal forces, and the net force in the entire SYSTEM is still 0. Let say that ...
... external forces exerting on it. What is the impact of Newton’s 3rd Law? If particle#1 exerts force on particle #2, there must be another force that the particle #2 exerts on #1 as the reaction force. Both the forces are internal forces, and the net force in the entire SYSTEM is still 0. Let say that ...
Non-Linear Motion
... • The vertical distance the cannonball falls at any point beneath this imaginary dashed line is the same vertical distance it would fall if it were dropped from rest and had been falling the same amount of time. • Recall that this distance is given by d = ½gt2, where t is the elapsed time. • Roundin ...
... • The vertical distance the cannonball falls at any point beneath this imaginary dashed line is the same vertical distance it would fall if it were dropped from rest and had been falling the same amount of time. • Recall that this distance is given by d = ½gt2, where t is the elapsed time. • Roundin ...
Physics 1. Mechanics Problems
... A hollow cylinder is sliding without friction (no rolling) with the velocity v. The cylinder comes to a surface with friction. What is the final velocity of the cylinder ? Solution. When the cylinder comes to the surface with friction it is decelerated by the friction force and at the same time its ...
... A hollow cylinder is sliding without friction (no rolling) with the velocity v. The cylinder comes to a surface with friction. What is the final velocity of the cylinder ? Solution. When the cylinder comes to the surface with friction it is decelerated by the friction force and at the same time its ...
The Geometry of Forces Along Equidistant Particle Paths
... Theorem 2. Let M be a space form with negative curvature K = −k 2 < 0, then the coupling force between two particles of mass m moving at speed v at a distance d/2 from the central inertial path is inward and is given by Fc = −2mv 2 k tanh(kd/2). We note that this force is essentially a result of the ...
... Theorem 2. Let M be a space form with negative curvature K = −k 2 < 0, then the coupling force between two particles of mass m moving at speed v at a distance d/2 from the central inertial path is inward and is given by Fc = −2mv 2 k tanh(kd/2). We note that this force is essentially a result of the ...
Science 20 Unit b Final Test
... front of him and stops in the middle of the highway if it takes Drayton 0.4 seconds to respond and 4 seconds to come to a complete stop will he hit the deer? And if he doesn’t hit the deer how many meters is Drayton away from the deer? a. He hits the deer b. He stops 66.7 m from the deer c. He stops ...
... front of him and stops in the middle of the highway if it takes Drayton 0.4 seconds to respond and 4 seconds to come to a complete stop will he hit the deer? And if he doesn’t hit the deer how many meters is Drayton away from the deer? a. He hits the deer b. He stops 66.7 m from the deer c. He stops ...
Energy Methods - MIT OpenCourseWare
... Lagrange’s equations. They are the beginning of a complex, more mathematical approach to mechanics called analytical dynamics. In this course we will only deal with this method at an elementary level. Even at this simplified level, it is clear that considerable simplification occurs in deriving the eq ...
... Lagrange’s equations. They are the beginning of a complex, more mathematical approach to mechanics called analytical dynamics. In this course we will only deal with this method at an elementary level. Even at this simplified level, it is clear that considerable simplification occurs in deriving the eq ...
Brownian motion

Brownian motion or pedesis (from Greek: πήδησις /pˈɪːdiːsis/ ""leaping"") is the random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collision with the quick atoms or molecules in the gas or liquid. Wiener Process refers to the mathematical model used to describe such Brownian Motion, which is often called a particle theoryThis transport phenomenon is named after the botanist Robert Brown. In 1827, while looking through a microscope at particles trapped in cavities inside pollen grains in water, he noted that the particles moved through the water but was not able to determine the mechanisms that caused this motion. Atoms and molecules had long been theorized as the constituents of matter, and many decades later, Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules. This explanation of Brownian motion served as definitive confirmation that atoms and molecules actually exist, and was further verified experimentally by Jean Perrin in 1908. Perrin was awarded the Nobel Prize in Physics in 1926 ""for his work on the discontinuous structure of matter"" (Einstein had received the award five years earlier ""for his services to theoretical physics"" with specific citation of different research). The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.The mathematical model of Brownian motion has numerous real-world applications. For instance, Stock market fluctuations are often cited, although Benoit Mandelbrot rejected its applicability to stock price movements in part because these are discontinuous.Brownian motion is among the simplest of the continuous-time stochastic (or probabilistic) processes, and it is a limit of both simpler and more complicated stochastic processes (see random walk and Donsker's theorem). This universality is closely related to the universality of the normal distribution. In both cases, it is often mathematical convenience, rather than the accuracy of the models, that motivates their use.