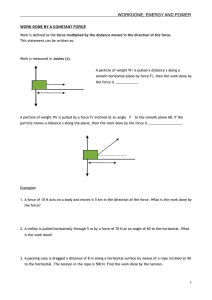
8-2 Simple Harmonic Motion 8-3 The Force Law for Simple
... A rod and a vane (massless) is fixed to the block. The vane is submerged in a liquid. As the vane moves up and down, the liquid exerts a drag force on the osillating system. The forces acting on the system: damping force Fd bv (for small v) (8-37) b is a damping constant. SI unit: kg/s Newton’s s ...
... A rod and a vane (massless) is fixed to the block. The vane is submerged in a liquid. As the vane moves up and down, the liquid exerts a drag force on the osillating system. The forces acting on the system: damping force Fd bv (for small v) (8-37) b is a damping constant. SI unit: kg/s Newton’s s ...
Ch-9 Force and Laws Of Motion.
... 2. The velocity of the ball changes four times. (i) As a football player kicks the football, its speed changes from zero to a certain value. As a result, the velocity of the ball gets changed. In this case, the force is applied by the kick of the player. (ii) When the ball reaches another player, he ...
... 2. The velocity of the ball changes four times. (i) As a football player kicks the football, its speed changes from zero to a certain value. As a result, the velocity of the ball gets changed. In this case, the force is applied by the kick of the player. (ii) When the ball reaches another player, he ...
ExcelSession3
... • Limit of demand = 1600 (May differ plus or minus 40%, not less than (Demand(10)+100)) • Annual volatility is 10% Link for Excel: http://ardent.mit.edu/real_options/ROcse_Excel_latest/Session3-2.xls ESD.70J Engineering Economy Module - Session 3 ...
... • Limit of demand = 1600 (May differ plus or minus 40%, not less than (Demand(10)+100)) • Annual volatility is 10% Link for Excel: http://ardent.mit.edu/real_options/ROcse_Excel_latest/Session3-2.xls ESD.70J Engineering Economy Module - Session 3 ...
- TestbankU
... 5) Why is it so difficult to remove the lid from a vacuum-sealed jar? A) The air pressure outside the jar pushes downward on the lid more strongly than the air pressure inside pushes upward on the lid. B) The vacuum inside the jar pushes outward on the lid, holding it firmly to the jar. C) The vacuu ...
... 5) Why is it so difficult to remove the lid from a vacuum-sealed jar? A) The air pressure outside the jar pushes downward on the lid more strongly than the air pressure inside pushes upward on the lid. B) The vacuum inside the jar pushes outward on the lid, holding it firmly to the jar. C) The vacuu ...
Oscillations
... Find the probability d p(x) of finding the particle between x and x + dx. 6.20 Using the probability density distribution for the SHO, calculate the mean potential energy and the mean kinetic energy over an oscillation. ...
... Find the probability d p(x) of finding the particle between x and x + dx. 6.20 Using the probability density distribution for the SHO, calculate the mean potential energy and the mean kinetic energy over an oscillation. ...
Applied Maths Introductory Module Workbook
... A car of mass 150kg is accelerating in a race. If the car engine provides a thrust of 200N, and the drag, or resistance, is 180N find i) The net force in the direction of motion ii) The acceleration of the car iii) The speed of the car after travelling 100m, assuming the car starts from rest. iv) If ...
... A car of mass 150kg is accelerating in a race. If the car engine provides a thrust of 200N, and the drag, or resistance, is 180N find i) The net force in the direction of motion ii) The acceleration of the car iii) The speed of the car after travelling 100m, assuming the car starts from rest. iv) If ...
Circular Motion
... center of the circle is called the centripetal force To analyze centripetal acceleration situations accurately, you must identify the agent of the force that causes the acceleration (such as tension on a string). Then you can apply Newton’s second law for the component in the direction of the accele ...
... center of the circle is called the centripetal force To analyze centripetal acceleration situations accurately, you must identify the agent of the force that causes the acceleration (such as tension on a string). Then you can apply Newton’s second law for the component in the direction of the accele ...
Oscillations
... 17. Which of the following is true for both spheres? (A) The maximum kinetic energy is attained as the sphere passes through its equilibrium position (B) The maximum kinetic energy is attained as the sphere reaches its point of release. (C) The minimum gravitational potential energy is attained as t ...
... 17. Which of the following is true for both spheres? (A) The maximum kinetic energy is attained as the sphere passes through its equilibrium position (B) The maximum kinetic energy is attained as the sphere reaches its point of release. (C) The minimum gravitational potential energy is attained as t ...
Average Acceleration Instantaneous Acceleration
... The gravitational acceleration (g) is the acceleration due to the gravitational force, on earth, its magnitude is approximately 9.8 ms-2. The gravitational force always points downward, therefore the direction of g is always downward. An object moving downward under the gravitational pull has g = + ...
... The gravitational acceleration (g) is the acceleration due to the gravitational force, on earth, its magnitude is approximately 9.8 ms-2. The gravitational force always points downward, therefore the direction of g is always downward. An object moving downward under the gravitational pull has g = + ...
lecture 10
... plane of angle a: Scleronomic (constraint does not involve time) Non-holonomic (cylinder leaves the inclined plane at some point) Conservative (gravitational force acting is derivable from a potential) A sphere rolling down another sphere which is rolling with a uniform speed along a horizontal plan ...
... plane of angle a: Scleronomic (constraint does not involve time) Non-holonomic (cylinder leaves the inclined plane at some point) Conservative (gravitational force acting is derivable from a potential) A sphere rolling down another sphere which is rolling with a uniform speed along a horizontal plan ...
Brownian motion

Brownian motion or pedesis (from Greek: πήδησις /pˈɪːdiːsis/ ""leaping"") is the random motion of particles suspended in a fluid (a liquid or a gas) resulting from their collision with the quick atoms or molecules in the gas or liquid. Wiener Process refers to the mathematical model used to describe such Brownian Motion, which is often called a particle theoryThis transport phenomenon is named after the botanist Robert Brown. In 1827, while looking through a microscope at particles trapped in cavities inside pollen grains in water, he noted that the particles moved through the water but was not able to determine the mechanisms that caused this motion. Atoms and molecules had long been theorized as the constituents of matter, and many decades later, Albert Einstein published a paper in 1905 that explained in precise detail how the motion that Brown had observed was a result of the pollen being moved by individual water molecules. This explanation of Brownian motion served as definitive confirmation that atoms and molecules actually exist, and was further verified experimentally by Jean Perrin in 1908. Perrin was awarded the Nobel Prize in Physics in 1926 ""for his work on the discontinuous structure of matter"" (Einstein had received the award five years earlier ""for his services to theoretical physics"" with specific citation of different research). The direction of the force of atomic bombardment is constantly changing, and at different times the particle is hit more on one side than another, leading to the seemingly random nature of the motion.The mathematical model of Brownian motion has numerous real-world applications. For instance, Stock market fluctuations are often cited, although Benoit Mandelbrot rejected its applicability to stock price movements in part because these are discontinuous.Brownian motion is among the simplest of the continuous-time stochastic (or probabilistic) processes, and it is a limit of both simpler and more complicated stochastic processes (see random walk and Donsker's theorem). This universality is closely related to the universality of the normal distribution. In both cases, it is often mathematical convenience, rather than the accuracy of the models, that motivates their use.