Rules of Inference and Methods of Proof
... of the previous ones. The body of any argument can be divided into two parts: - Premises: all but the final proposition in the argument. - Conclusion: the final proposition of the argument. So, to show the validity of any argument we show that the conclusion of the argument must follow from the trut ...
... of the previous ones. The body of any argument can be divided into two parts: - Premises: all but the final proposition in the argument. - Conclusion: the final proposition of the argument. So, to show the validity of any argument we show that the conclusion of the argument must follow from the trut ...
Introduction to Logic
... Formal Language • Formal logic replaces the ordinary language of argument with a symbolic language. • This language is meant to be free of all ambiguity and vagueness. • The language is meant to wear its logical structure on its face. • Our formal languages: SL and QL. ...
... Formal Language • Formal logic replaces the ordinary language of argument with a symbolic language. • This language is meant to be free of all ambiguity and vagueness. • The language is meant to wear its logical structure on its face. • Our formal languages: SL and QL. ...
Yablo`s paradox
... ¬Tsn is provable for all n is that we have a uniform proof, i.e., a proof for variable n. Moreover, no finite reasoner ever really applies the ω-rule. The only way that they can know that there is a proof of each α(i) is because they have a uniform method of constructing such proofs. And it is this ...
... ¬Tsn is provable for all n is that we have a uniform proof, i.e., a proof for variable n. Moreover, no finite reasoner ever really applies the ω-rule. The only way that they can know that there is a proof of each α(i) is because they have a uniform method of constructing such proofs. And it is this ...
1 Proof of set properties, concluded
... So far we have seen two proof techniques for proving a statement of the form P ⇒ Q: Direct proof Assume P ; argue by logical steps to Q. Contrapositive Assume ¬Q; argue by logical steps to ¬P . However there is a third technique, which shares particular elements with the contrapositive. Recall that, ...
... So far we have seen two proof techniques for proving a statement of the form P ⇒ Q: Direct proof Assume P ; argue by logical steps to Q. Contrapositive Assume ¬Q; argue by logical steps to ¬P . However there is a third technique, which shares particular elements with the contrapositive. Recall that, ...
Section 3.6: Indirect Argument: Contradiction and Contraposition
... So far, we have only considered so called “direct proofs” of mathematical statements. Specifically, we have been given a statement to prove, and then we have used the definitions and previous results to logically derive the statement. In this section we consider “indirect proofs” proofs which do not ...
... So far, we have only considered so called “direct proofs” of mathematical statements. Specifically, we have been given a statement to prove, and then we have used the definitions and previous results to logically derive the statement. In this section we consider “indirect proofs” proofs which do not ...
Lecturecise 19 Proofs and Resolution Compactness for
... First-order logic allows arbitrary relations and functions (they are defined only through their axioms) Useful for modeling all of math (e.g. through set theory axioms), and thus in principle applies to all program verification problems as well. To prove whether a property holds: I describe the prop ...
... First-order logic allows arbitrary relations and functions (they are defined only through their axioms) Useful for modeling all of math (e.g. through set theory axioms), and thus in principle applies to all program verification problems as well. To prove whether a property holds: I describe the prop ...
com.1 The Compactness Theorem
... Problem com.2. In the standard model of arithmetic N, there is no element k ∈ |N| which satisfies every formula n < x (where n is 0...0 with n 0’s). Use the compactness theorem to show that the set of sentences in the language of arithmetic which are true in the standard model of arithmetic N are a ...
... Problem com.2. In the standard model of arithmetic N, there is no element k ∈ |N| which satisfies every formula n < x (where n is 0...0 with n 0’s). Use the compactness theorem to show that the set of sentences in the language of arithmetic which are true in the standard model of arithmetic N are a ...
CS 2742 (Logic in Computer Science) Lecture 6
... This is another way to describe “proof by contrapositive”. Similarly we can write the proof by cases, by contradiction, by transitivity and so on. They can be derived from the original logic identities. For example, modus ponens becomes ((p → q) ∧ p) → q. ...
... This is another way to describe “proof by contrapositive”. Similarly we can write the proof by cases, by contradiction, by transitivity and so on. They can be derived from the original logic identities. For example, modus ponens becomes ((p → q) ∧ p) → q. ...
Gresham Ideas - Gresham College
... impossible. You might think that in an ideal world there would be no paradoxes. But in that case medical care would be rather limited, because in such an ideal world there can only be one doctor! Why? Because if there are two doctors then we have a pair o’ docs – and we said there can be no paradox ...
... impossible. You might think that in an ideal world there would be no paradoxes. But in that case medical care would be rather limited, because in such an ideal world there can only be one doctor! Why? Because if there are two doctors then we have a pair o’ docs – and we said there can be no paradox ...
Solutions for Exam 1 - University of Hawaii Mathematics
... Since the last two columns are identical, A ∩ B = A ∪ B. 6. Determine whether the following argument is valid. Name the rule of inference or the fallacy. If n is a real number such that n > 2, then n2 > 4. Suppose that n ≤ 2. Then n2 ≤ 4. This is the fallacy of denying the hypothesis, so the argumen ...
... Since the last two columns are identical, A ∩ B = A ∪ B. 6. Determine whether the following argument is valid. Name the rule of inference or the fallacy. If n is a real number such that n > 2, then n2 > 4. Suppose that n ≤ 2. Then n2 ≤ 4. This is the fallacy of denying the hypothesis, so the argumen ...
p - Upm
... time, then the New Year’s party would have been canceled and Alicia would have been angry. If the party were canceled, then refunds would have had to be made. No refunds were made. Therefore the band could play rock music. First we convert the given argument into symbolic form by using the following ...
... time, then the New Year’s party would have been canceled and Alicia would have been angry. If the party were canceled, then refunds would have had to be made. No refunds were made. Therefore the band could play rock music. First we convert the given argument into symbolic form by using the following ...
on Computability
... Godel's Second Incompleteness Theorem. In any consistent axiomatizable theory (axiomatizable means the axioms can be computably generated) which can encode sequences of numbers (and thus the syntactic notions of "formula", "sentence", "proof") the consistency of the system is not provable in the sys ...
... Godel's Second Incompleteness Theorem. In any consistent axiomatizable theory (axiomatizable means the axioms can be computably generated) which can encode sequences of numbers (and thus the syntactic notions of "formula", "sentence", "proof") the consistency of the system is not provable in the sys ...
Methods of Proof for Boolean Logic
... Why truth tables are not sufficient: • Exponential sizes • Inapplicability beyond Boolean connectives ...
... Why truth tables are not sufficient: • Exponential sizes • Inapplicability beyond Boolean connectives ...
Methods of Proof for Boolean Logic
... Why truth tables are not sufficient: • Exponential sizes • Inapplicability beyond Boolean connectives ...
... Why truth tables are not sufficient: • Exponential sizes • Inapplicability beyond Boolean connectives ...
Comments on the use of the pumping lemma for regular languages
... inequalities), and without regard to the value of m, we can find some specific pumping value i 0 (i 0 ), such that wi = xyiz L (the desired contradiction). If our counterexample does not lead to this contradiction, nothing is proven. Either the counterexample was not a good choice, or the lan ...
... inequalities), and without regard to the value of m, we can find some specific pumping value i 0 (i 0 ), such that wi = xyiz L (the desired contradiction). If our counterexample does not lead to this contradiction, nothing is proven. Either the counterexample was not a good choice, or the lan ...
Discrete Computational Structures (CS 225) Definition of Formal Proof
... 2. A result of applying one of the logical equivalency rules (text, p. 35) to a previous statement in the proof. 3. A result of applying one of the valid argument forms (text, p. 61) to one or more previous statements in the proof. ...
... 2. A result of applying one of the logical equivalency rules (text, p. 35) to a previous statement in the proof. 3. A result of applying one of the valid argument forms (text, p. 61) to one or more previous statements in the proof. ...
Reasoning without Contradiction
... argument, so it is reasonable to believe that tautologies are not required for reasoning. But contradictions, it seems, feature in tried and trusted proof procedures, so one might suppose that, were contradiction somehow banned from proof procedures, incompleteness would result. But I think that thi ...
... argument, so it is reasonable to believe that tautologies are not required for reasoning. But contradictions, it seems, feature in tried and trusted proof procedures, so one might suppose that, were contradiction somehow banned from proof procedures, incompleteness would result. But I think that thi ...
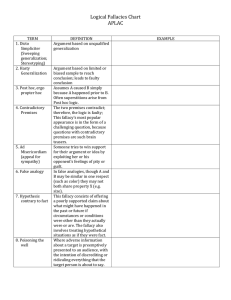
Logical Fallacies Chart APLAC TERM DEFINITION EXAMPLE 1
... The two premises contradict; therefore, the logic is faulty; This fallacy's most popular appearance is in the form of a challenging question, because questions with contradictory premises are such brain teasers. Someone tries to win support for their argument or idea by exploiting her or his opponen ...
... The two premises contradict; therefore, the logic is faulty; This fallacy's most popular appearance is in the form of a challenging question, because questions with contradictory premises are such brain teasers. Someone tries to win support for their argument or idea by exploiting her or his opponen ...
The Ontological argument 2
... female monarch’ 2) To explain there actually is something: ‘there is such a thing as a vampire’. ...
... female monarch’ 2) To explain there actually is something: ‘there is such a thing as a vampire’. ...
The Ontological argument 2
... female monarch’ 2) To explain there actually is something: ‘there is such a thing as a vampire’. ...
... female monarch’ 2) To explain there actually is something: ‘there is such a thing as a vampire’. ...
Name MAT101 – Survey of Mathematical Reasoning Professor
... from the Mesozoic era, then it is not from the Crestaceous period. If the fossil is from the Mesozoic era, then it is at least 65 million years old. Therefore, if the fossil is an ammonite, it is at least 65 million years old.” ...
... from the Mesozoic era, then it is not from the Crestaceous period. If the fossil is from the Mesozoic era, then it is at least 65 million years old. Therefore, if the fossil is an ammonite, it is at least 65 million years old.” ...
Compactness Theorem for First-Order Logic
... Let G be any set of formulas of first-order logic. Then G is satisfiable if every finite subset of G is satisfiable. ...
... Let G be any set of formulas of first-order logic. Then G is satisfiable if every finite subset of G is satisfiable. ...
The Ontological Argument Part 2 File
... female monarch’ 2) To explain there actually is something: ‘there is such a thing as a vampire’. ...
... female monarch’ 2) To explain there actually is something: ‘there is such a thing as a vampire’. ...