Lecture 34
... Example: Displacement measurement Given: The pulse-echo ultrasonic transducer in the ME 345 lab is used to measure the thickness of a piece of aluminum. The transmitted and reflected signals are read by an oscilloscope. The speed of sound in the aluminum is a = 6300 m/s. To do: Sketch the oscillosc ...
... Example: Displacement measurement Given: The pulse-echo ultrasonic transducer in the ME 345 lab is used to measure the thickness of a piece of aluminum. The transmitted and reflected signals are read by an oscilloscope. The speed of sound in the aluminum is a = 6300 m/s. To do: Sketch the oscillosc ...
milgram-levels-of-measurement
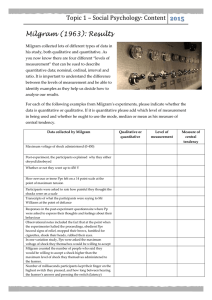
... you now know there are four different “levels of measurement” that can be sued to describe quantitative data; nominal, ordinal, interval and ratio. It is important to understand the difference between the levels of measurement and be able to identify examples as they help us decide how to analyse ou ...
... you now know there are four different “levels of measurement” that can be sued to describe quantitative data; nominal, ordinal, interval and ratio. It is important to understand the difference between the levels of measurement and be able to identify examples as they help us decide how to analyse ou ...
Dimensional Analysis (The Factor Label Method)
... Dimensional Analysis (The Factor Label Method) Most calculations in science involve measured quantities. In such calculations, the units in which quantities are measured must be treated mathematically just as the numerical parts of the quantities are. For example, in multiplying 1.2 cm by 2.0 cm, th ...
... Dimensional Analysis (The Factor Label Method) Most calculations in science involve measured quantities. In such calculations, the units in which quantities are measured must be treated mathematically just as the numerical parts of the quantities are. For example, in multiplying 1.2 cm by 2.0 cm, th ...
Types of question
... Q30. Which new drugs or new patterns of use have been reported? Q13. Indicate primary substance of abuse, that is, the most frequently used Other (specify): …………………….. ...
... Q30. Which new drugs or new patterns of use have been reported? Q13. Indicate primary substance of abuse, that is, the most frequently used Other (specify): …………………….. ...
Chapter 11 quantitative data
... • Typically used with interval and ratio levels of measurement • A measure of association between two variables that also indicates direction and strength of the relationship – r=0 (no relationship), r=1.00 (perfect relationship) – A +r value (a direct relationship), -r value (an inverse relationshi ...
... • Typically used with interval and ratio levels of measurement • A measure of association between two variables that also indicates direction and strength of the relationship – r=0 (no relationship), r=1.00 (perfect relationship) – A +r value (a direct relationship), -r value (an inverse relationshi ...