... FIG. 4: Experimental NMR spectra and respective tomographed density matrices, for the four bell states, as indicated on the figure. FIG. 3: Experimental NMR spectra and respective tomographed density matrices, for (a) before and after the operation HB |00i = √1 [|00i + |01i] (Hadamard gate applied t ...
Brief Biography of names i
... development was carried out by George de la Warr in the UK, and Dr. Ruth Drown. http://issseem.org/onlinedocs/Maret-Karl-EnergyMedicineinAmerica-July-09.doc.pdf Juan Acosta-Urquidi PhD After more than 20 years of basic laboratory research in cellular neurophysiology, he joined an NIH-funded project ...
... development was carried out by George de la Warr in the UK, and Dr. Ruth Drown. http://issseem.org/onlinedocs/Maret-Karl-EnergyMedicineinAmerica-July-09.doc.pdf Juan Acosta-Urquidi PhD After more than 20 years of basic laboratory research in cellular neurophysiology, he joined an NIH-funded project ...
Quantum correlations
... von Neumann entropy S(̺) = Tr̺ log ̺: measures how broadly ̺ is spread over the Hilbert space For correlated states I > 0: the global state is known with more accuracy than ose of the single parts ...
... von Neumann entropy S(̺) = Tr̺ log ̺: measures how broadly ̺ is spread over the Hilbert space For correlated states I > 0: the global state is known with more accuracy than ose of the single parts ...
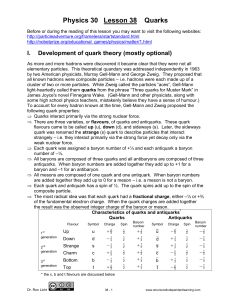
Chapter 2 ATOMIC THEORY
... 1923) discovered a new type of radiation called X-rays, and their ability to penetrate highly dense materials. Soon after the discovery of X-rays, Henri Becquerel (1852–1908) showed that certain materials emit similar rays independent of any external force. Such emission of radiation became known as ...
... 1923) discovered a new type of radiation called X-rays, and their ability to penetrate highly dense materials. Soon after the discovery of X-rays, Henri Becquerel (1852–1908) showed that certain materials emit similar rays independent of any external force. Such emission of radiation became known as ...
Spinons and triplons in spatially anisotropic frustrated antiferromagnets ARTICLES MASANORI KOHNO
... antiferromagnets. Note that the two-spinon approximation is not a low-energy one (unlike the familiar and powerful ‘bosonization’ technique) as it includes spinons with energies reaching up to πJ /2 J 0 . This is essential for comparison with inelastic neutron scattering data which extends over th ...
... antiferromagnets. Note that the two-spinon approximation is not a low-energy one (unlike the familiar and powerful ‘bosonization’ technique) as it includes spinons with energies reaching up to πJ /2 J 0 . This is essential for comparison with inelastic neutron scattering data which extends over th ...
Density Matrix Calculation of Surface Enhanced
... Raman scattering.11,25 In contrast, a1 mode enhancement was ascribed strictly to electromagnetic effects (A-term scattering). In more recent off-resonant experiments, Jackson, et al.,5,6 have measured SERS response of PMA-coated nanoshells under carefully controlled conditions with 782 nm (1.6 eV) ...
... Raman scattering.11,25 In contrast, a1 mode enhancement was ascribed strictly to electromagnetic effects (A-term scattering). In more recent off-resonant experiments, Jackson, et al.,5,6 have measured SERS response of PMA-coated nanoshells under carefully controlled conditions with 782 nm (1.6 eV) ...
Document
... a) The SI unit of the electric field is the newton per meter (N/m) b) The electric field is a vector quantity. c) At a given point, a charged particle will experience a force, if an electric field is present at that location. d) If a positively-charged particle is placed at a location where the elec ...
... a) The SI unit of the electric field is the newton per meter (N/m) b) The electric field is a vector quantity. c) At a given point, a charged particle will experience a force, if an electric field is present at that location. d) If a positively-charged particle is placed at a location where the elec ...
Renormalization

In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities.Renormalization specifies relationships between parameters in the theory when the parameters describing large distance scales differ from the parameters describing small distances. Physically, the pileup of contributions from an infinity of scales involved in a problem may then result in infinities. When describing space and time as a continuum, certain statistical and quantum mechanical constructions are ill defined. To define them, this continuum limit, the removal of the ""construction scaffolding"" of lattices at various scales, has to be taken carefully, as detailed below.Renormalization was first developed in quantum electrodynamics (QED) to make sense of infinite integrals in perturbation theory. Initially viewed as a suspect provisional procedure even by some of its originators, renormalization eventually was embraced as an important and self-consistent actual mechanism of scale physics in several fields of physics and mathematics. Today, the point of view has shifted: on the basis of the breakthrough renormalization group insights of Kenneth Wilson, the focus is on variation of physical quantities across contiguous scales, while distant scales are related to each other through ""effective"" descriptions. All scales are linked in a broadly systematic way, and the actual physics pertinent to each is extracted with the suitable specific computational techniques appropriate for each.